我们用软件编程的时候，用到除法的时候，一个/这样的除号就搞定了。但是如果用硬件来实现除法，又是怎么样实现的了。

       计算机存储的数都是以二进制数来存储的，二进制的除法和我们平常用到十进制除法是一样的。辗转相除法。

       计算如上图，从最高位开始计算，如果大于除法，商为1。然后算下一位。知道算到最后一位，最后剩的结果为余数。

       原理是很简单的，但是实现起来，还是有点麻烦的。下面就编写代码来实现硬件的除法。

       这里输入的除数和被除数都是8位的数。简单考虑，都是无符号数。即不考虑数据正负。输出的商和余数也都是8位表示。

        从以上的图片计算，我们可看出，计算是首先将除数和被除数的最高的三位，比较，如果小于，则对应计算出来的商为1，然后被除数要减去除数，否则为0。然后再将除数和被除数的后面三位在比较，依次与被除数的最后3位比较完，输出最后的结果。

        而这里，我们采用的方法是，将被除数，扩展成16位的数据，低8位为被除数的值，高八位的值全为0。有开始信号，对16位数据data赋值，然后开始运算。比较data的高八位和除数的值，如果大于0，说明被除数大，将此时商置1，赋值给data的最低位，然后将被除数减去除数。然后将data向左移位一位，继续比较。最终计算8次后。Data的高8位数据就为所求的余数，低八位就为所求的商。

        下面举个例子说明：

        初始：输入被除数的值为78，输入除数的值为34

计算完后，输出的商就为2(00000010)，余数为10。计算正确。

代码如下，所示：

`timescale 1ns / 1ps

module divison

#(

         parameter W = 16, //扩展的位数

         parameter N = 8 //输入的除数和被除数的位数

  )

(

         input                      clk,

         input                      rst_n,

         input [N-1:0]          dividend,

         input [N-1:0]          divisor,

         input                       start,

         output wire [N-1:0] quotient,

         output wire [N-1:0] remainder,

         output reg              ready,

         output reg              busy,

         output reg              finish

  );

parameter idle = 3'b000;

parameter start_div = 3'b001;

parameter shift = 3'b010;

parameter done = 3'b110;

reg[2:0]             state;

reg[2:0]             state_next;

reg[W-1:0]        data;

reg[W-1:0]        data_next;

reg[N-1:0]         n_reg; //存储计算的次数

reg[N-1:0]         n_next;

always@(posedge clk) begin

if(!rst_n)

    begin

        state <= idle;

        data_next <= 0;

        n_reg <= 0;

    end

else

   begin

        state <= state_next;

        data <= data_next;

        n_reg <= n_next;

             end

end

always@* begin

state_next = state ;

data_next=data;

n_next = n_reg;

ready = 1;

busy = 0;

finish = 0;

case(state)

idle:

    begin

     data = 0;

     if( start == 1 && busy !=0 ) //只有在空闲状态，开始信号才有效。

           begin

                  state_next = shift;

                  data_next = {{W-N{1'b0}},dividend};

                   n_next = N;

           end

    end

shift:

    begin

           data_next = {data[W-2:0],1'b0};

            busy = 1;

            ready = 0;

            n_next = n_reg - 1'b1;

            if(data_next[W-1:N] >= divisor)

                   begin

                         data_next[0] = 1;

                          data_next[W-1:N] = data_next[W-1:N] - divisor;

                  end

           if(n_reg==1)

                   state_next = done;

   end

done:

    begin

           finish = 1;

           state_next = idle;

    end

endcase

end

assign quotient   = finish ? data[N-1:0] : quotient;

assign remainder = finish ? data[W-1:N] : remainder;

endmodule

      代码，比较简单，只要知道了原理，代码是很好编写的。主要是要理解将被除数扩展为16位。然后再计算。

      编写测试代码，测试：

reg[5:0] i;

   always #1 clk = ~clk;
initial begin
// Initialize Inputs
clk = 0;
rst_n = 0;
dividend = 12;
divisor = 123;
start = 0;

  
// Wait 100 ns for global reset to finish
#100  rst_n = 1;
   start = 1;

for(i=0;i<=32;i=i+1)
 begin
    dividend = {$random}%256 ;
    divisor = {$random}%256;
start = 1;
           @(finish);
 end
// Add stimulus here

end

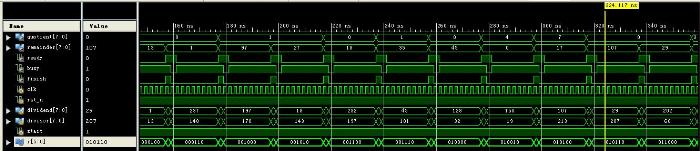
仿真图如下所示。

        从仿真图中，可看出，输出结果在，在8个时钟周期后，输出最终的计算结果。