使用乘法器实现各种移位操作
0赞昨天看了一本书,使用乘法器来实现各种移位操作。包括逻辑左移,逻辑右移,算术右移,循环右移。
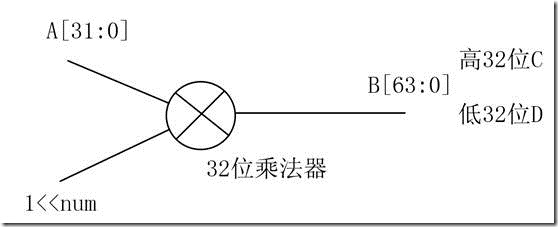
实现的框图如下所示:考虑对32位数据处理
核心器件就是一个乘法器。
a是输入的32位数据,
num是移位的5位数据
b是乘法器的64位输出
下面是实现各种移位的算法:
1、 逻辑左移:结果取D
2、 逻辑右移:num取反加1,结果取C
3、 算术右移:num取反加1,结果取C。如果A[31]为1,A取反,在对结果C取反即可。为0,结果取C。
4、 循环右移:num取反加1,结果取C|D。
看似是很简单的,而且算法也还是挺奇特的。以前还没有发现,还可以用乘法器来实现移位。
下面用verilog写程序进行验证。
代码也比较简单,对输入进行选择,对输出进行选择,然后中间一个乘法器。硬件电路大致为:
有了这个图,写代码就更容易了。
module shitf_according_mul(
input [31:0] a,
input [4:0] num,
input [1:0] shift_mode,
output reg[31:0] out
);
localparam logic_left_shift = 2'b00;
localparam logic_right_shift = 2'b01;
localparam cycle_right_shift = 2'b10;
localparam airth_right_shift = 2'b11;
//data
reg [31:0] reg_a;
always@(*) begin
case(shift_mode)
logic_left_shift:
reg_a = a;
logic_right_shift:
reg_a = a;
cycle_right_shift:
reg_a = a;
airth_right_shift:
reg_a = a[31] ? ~a:a;
endcase
end
//shift number
reg [31:0] reg_num;
always@* begin
case(shift_mode)
logic_left_shift:
reg_num = 32'b1<<num;
logic_right_shift:
reg_num = 32'b1<<(~num + 1'b1);
cycle_right_shift:
reg_num = 32'b1<<(~num + 1'b1);
airth_right_shift:
reg_num = 32'b1<<(~num + 1'b1);
endcase
end
//mul
wire [63:0] mul_o;
assign mul_o = reg_a * reg_num;
//out
always@* begin
case(shift_mode)
logic_left_shift:
out = mul_o[31:0];
logic_right_shift:
out = mul_o[63:32];
cycle_right_shift:
out = mul_o[31:0] | mul_o[63:32];
airth_right_shift:
out = a[31] ? ~mul_o[63:32]:mul_o[63:32];
endcase
end
endmodule
纯组合逻辑设计,设计好了,需要写testbench验证吧。Testbench编写,也比较简单,就给输入和移位的值以及移位模式随便赋值就行了。
核心代码就是
shift_mode = logic_left_shift;
for(j=0; j<=10; j=j+1) begin
a = {$random()};
for(i=0; i<=31; i=i+1)
begin
num = i;
#100;
end
end
shift_mode = logic_right_shift;
for(j=0; j<=10; j=j+1) begin
a = {$random()};
for(i=0; i<=31; i=i+1)
begin
num = i;
#100;
end
end
shift_mode = cycle_right_shift;
for(j=0; j<=10; j=j+1) begin
a = {$random()};
for(i=0; i<=31; i=i+1)
begin
num = i;
#100;
end
end
shift_mode = airth_right_shift;
for(j=0; j<=10; j=j+1) begin
a = {$random()};
for(i=0; i<=31; i=i+1)
begin
num = i;
#100;
end
end
每组移位测试10次,输入使用随机数产生,移位的值使用for循环从0遍历到31。好,开仿。
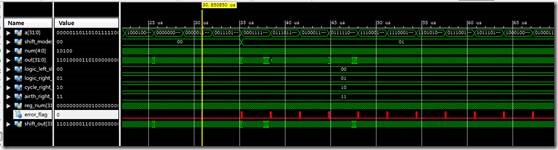
波形图如下所示:
这有输出了,但是这看着也太蛋疼了。这怎么验证,32位数据。对比输出和输入都对比得要死了。
这个时候,就要用到自动比对了。因为电路的功能是确定的,所以我们肯定知道对应不同的输入,输出应该是什么。我们可以通过其他方法,得到输出的值,然后和仿真得到的结果进行比对,如果是一样的话,就说明电路功能是正确的,如果不一样的话,就说明电路设计就有问题了。
在testbench中加入自动比对的代码。既然要自动比对,首先要得到输入对应的输出。移位,用代码写是比较简单的。
这样,就得到了输出值了。
然后是比对,比对的话,就比较计算出来的输出和电路的输出是否一样,一样的话说明正确。这里就用一个信号来表示。
//`define no_delay_detect
`ifdef no_delay_detect
wire error_flag;
assign error_flag = ((out != shift_out )? 1 : 0);
`else
reg error_flag;
always@(*) begin
#1;
if(out != shift_out)
error_flag = 1;
else
error_flag = 0;
end
`endif
always@(posedge error_flag) begin
if(error_flag==1)
$display("a=%b j=%d num=%d shift_mode=%d out=%b",a,j,num,shift_mode,out);
end
这里,用到了verilog的条件编译的一些知识。`ifdef这个和c语言中的#ifdef一样,`else和#else一样,最后的`endif和#endif是一样的。这个地方用到条件编译,是因为对应这两种比对方法,结果不一样的。第一种是没有加延时比对,第二种是加延时比对的。
最后一个always对标志进行判断,如果标志为1的话,就说明输出有错,将信息打印。否则就不打印。这里always的信号列表使用的是标志的上升沿。这样就保证了一次输入就检测一次。
先看一下使用第一个条件编译的仿真结果。就是不带延时的仿真。
波形中有标志信号有1,说明输出结果有的地方不对。
在看看打印信息。
发现,打印信息竟然在每一次输入变化的时候,都会有。这明显不对了。从波形图中看出,只是有的地方输出不正确,大多数地方是正确的。那么正确的地方应该是不会有打印信息的。
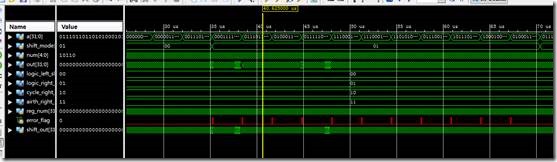
在来看看第二种条件编码仿真。即带延时的比对仿真。
波形图和上面那个一样,标志信号有的地方为1,说明输出不对。
但是看看打印信息。
发现,打印信息变少了,而且是在输出错误的地方才打印,输出正确的地方是没有打印的。
造成这两种不同的打印情况,是为什么了?这个和仿真器的仿真机制有关系的。Verilog的仿真是事件型的仿真,因为这是仿真硬件,而硬件是并行执行的。
在检测的always块中设置断点,看第一种条件编译仿真。
运行后,会在输入第一次变化的地方仿真暂停。看波形图。右边是波形,左边value是右边黄色标线出各个信号的值。
看出,在输入没有变化的时候,电路的输出和预想的输出是一样的,所以标志信号为0。所以仿真继续,不会停。但是在输入变化的时候,发现,电路的输出没有变,但是预想的输出已经变了,因为这个时候输入已经变了,所以一比对,发现电路输出和预想的输出不一样,然后标志置1。所以就触发了错误检测always块,所以程序就暂停了,然后就打印信息了。
原来问题就是在这里。在testbench中,信号的变化可以认为是没有延时的,输入一变化,输出马上就变化。但是在verilog的电路模块中,输出是有延时的,即不是输入一变化,输出就马上有。而是要经历一个很短暂的时间,输出才变化。
所以说,检测的时候,应该是在输入变化后的延时一段时间后检测才是正确的。所以才需要第二种条件编译仿真。带延时的检测。
有了这样一个自动比对,就不用一个一个的去看波形验证功能是否正确了。只需要去看标志为1的地方就行了。
定位到标志为1的地方。看出,移位的位数是0。移位方式是逻辑右移。电路的输出竟然是0。其实后面每一个出错的地方都是在移位的位数是0的地方。这是什么原因了?
其实是出现在以下的代码中
logic_right_shift:
reg_num = 32'b1<<(~num + 1'b1);
仿真的时候看到,当num为0的时候,reg_num为1。所以乘法的结果的高32位是为0的,所以输出才是0。
其实,当移位的位数为0的时候,输出就是输入本身。都不用对数据进行操作。所以使用乘法器构造移位,移位位数为0是比较特殊要考虑的。
可能大家觉得奇怪,为什么要用乘法器去构造移位器了,明显乘法器用的资源比普通的移位器用的资源多去了。而且还是32位乘法器。这个就得看具体的应用了。假设在一个设计中,乘法器是必须要使用的,那么用乘法器来实现移位就很有必要了。因为乘法器是必须要用的,那为什么还要花另外的逻辑去实现移位了。就好比夏天在一个空调房里面,空调是必须要开的,那肯定就不会有人傻到再去买一个风扇来用吧。