不知道为什么AET的网页这两天经常进不去，所以开始尝试着用open live writer来写博客，这是我open live writer 的处女作，也不知道效果怎么样，各位有兴趣的看官将就着看一看吧，嘻嘻。

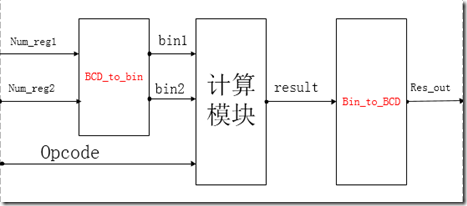
       这是计算器的最后一个模块了，前面分别总结了一下矩阵键盘扫描模块，数码管显示与消零模块，逐位输入与输出控制模块，可以说是万事具备，只欠东风了，今天就来总结一下这个东风吧。其实计算模块是比较简单的。大致框图如下

       从系统框图上我们大体可以看到，这个计算模块大体上包括一个BCD转二进制的模块，一个二进制转BCD的模块，以及一个计算模块。这一部分比较简单，几乎都是用组合逻辑完成的，没有用什么时序电路，当然这样一种方法比较占FPGA的逻辑资源，有很多地方可以去做一个优化。

       由我们的输入是以BCD码的形式保存的，但是计算的时候，FPGA是不会以BCD码的形式来进行计算。比如说，我们输入12这个数，它的BCD码的形式是0001_0010，但是他的二进制形式却是1100。如果我们直接拿BCD码去计算，FPGA会把它当作18。当然，如果你强行要用BCD码来进行计算，并想得出正确结果也并不是不可能，只是实现的难易程度上会差了好几个级别。所以我们在进行计算前，最好对操作数进行一个BCD转二进制的操作。

       最简单的BCD转二进制的方法是什么呢？

       我们知道BCD码每4位表示一个10进制数，我们现在假设num_reg是一个16位的BCD码，也就是4位的十进制数。那么num_reg[15:12]表示这个数的最高位，他的权值是1000，这个应该可以理解吧。同样的道理，num_reg[11:8]的权为100，num_reg[7:4]的权为10，num_reg[3:0]的权为1。

所以bin = num_reg[15:12] *1000 + num_reg[11:8]*100+num_reg[7:0]*10+num_reg[3:0]。

而在FPGA中是可以识别十进制的，这个模块与其说是BCD转二进制，倒不如说是BCD转十进制。反过来二进制转BCD怎么做，我相信大家都已经清楚了吧，我就不废话了。

      这种方法虽然可以实现功能，但是乘法和除法是非常的耗逻辑资源，如果是实际的工程中，这种方法肯定是不提倡使用的。如果不这样做，那我们还有什么方法呢？

      下面我们就介绍一种方法，只用加法就能解决掉BCD转二进制的问题。不知道大家知不知道二进制左移一位就相当于乘2。不知道也不要紧，我们先来简单证明一下：假如有一个二进制数abcd，转换成十进制等于a*8+b*4+c*2+d；左移一位后相当于abcd0，它的十进制等于a*16+b*8+c*4+d*2 =2(a*8+b*4+c*2+d)，所以abcd0 = 2*abcd。

       根据这种方法可以得到10*abcd = abcd0 + abcd000；是这样吧。

那么100 * abcd = abcd00 + abcd0_0000+abcd_000_000；同样的道理，乘1000，乘10000，我们都可以用这用方法来进行计算。整体的思路就是这个样子了。这种方法的代码写起来肯定会比上面那种要复杂一些，但是能够在很大程度上节省逻辑资源，有兴趣的小伙伴可以尝试着自己写一下。虽然我自己都没写。

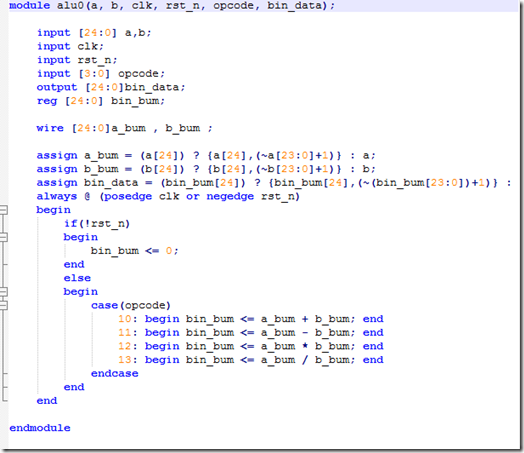
        下面再说一下计算模块，计算如果要实现负数的运算的话，最好是转换成补码进行计算。补码的转换方式其实很简单啦，一句话就搞定了。假如一个16位的二进制数，那么最高位是符号位，0为正1为负。assign num_bm = num[15] ? {num[15],(~num[14:0]+1)} : num; 另外补码的补码是原码，不知道大家是否知道这个规律呢。

最后，我们把代码简单的贴一下

一、计算器模块

在计算器的模块里面也还有很大的优化空间，前面已经说过了乘法的优化方法了，就是移位相加。那么除法怎么优化呢？我们可不可以把除数与被除数的关系转化为减速与被减数的关系呢，让被减数循环的减去减数，做一个计数，看减多少次之后被减数小于减数，俺么计数的值是不是就是我们要的商。当然我水平拙劣，肯定还有更好的优化方法，欢迎各位和我讨论。

由于第一次用open live writer，没找到上传附件的地方，下次登录网页再传工程源码。