利用quartus II 13.0例化了一个ALTFP_SINCOS

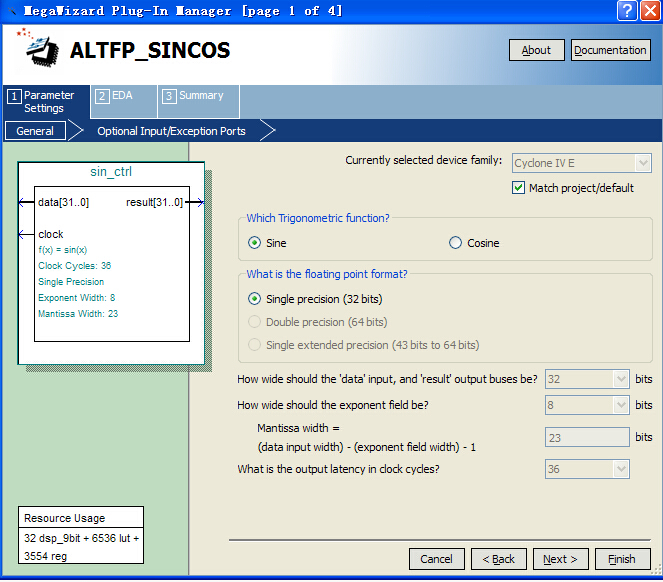
可是仿真出来的结果就是不对啊结果是32'b0和{31'b0,1'b1} 这是为什么呢？我输入无论是固定值还是计数器的值都是这个样子，咋回事呢？去官方论坛也有此问题的网友，手册介绍的也不够详细啊！关键是结果只有32'b0和{31'b0,1'b1}，郁闷。不甘心，于是搞了cordic算法-瑞士军刀！！！

16Bit精度--转自：http://www.cnblogs.com/aikimi7/p/3929592.html

8Bit精度--转自：http://www.cnblogs.com/qiweiwang/archive/2010/07/28/1787021.html

原理不说了，网上n++，最后贴上verilog源码及testbench

//360°--2^16,phase_in = 16bits (input [15:0] phase_in)
//1°--2^16/360
`define rot0  16'h2000    //45
`define rot1  16'h12e4    //26.5651
`define rot2  16'h09fb    //14.0362
`define rot3  16'h0511    //7.1250
`define rot4  16'h028b    //3.5763
`define rot5  16'h0145    //1.7899
`define rot6  16'h00a3    //0.8952
`define rot7  16'h0051    //0.4476
`define rot8  16'h0028    //0.2238
`define rot9  16'h0014    //0.1119
`define rot10 16'h000a    //0.0560
`define rot11 16'h0005    //0.0280
`define rot12 16'h0003    //0.0140
`define rot13 16'h0001    //0.0070
`define rot14 16'h0001    //0.0035
`define rot15 16'h0000    //0.0018

module cordic(
output reg  [16:0] sin,cos,eps,
input [15:0] phase_in,
input clk
);
parameter PIPELINE = 16;
//parameter K = 16'h4dba;//k=0.607253*2^15
parameter K = 16'h9b74;//gian k=0.607253*2^16,9b74,n means the number pipeline
//pipeline 16-level    //maybe overflow,matlab result not overflow
//MSB is signed bit,transform the sin and cos according to phase_in[15:14]
reg [16:0] x0=0,y0=0,z0=0;
reg [16:0] x1=0,y1=0,z1=0;
reg [16:0] x2=0,y2=0,z2=0;
reg [16:0] x3=0,y3=0,z3=0;
reg [16:0] x4=0,y4=0,z4=0;
reg [16:0] x5=0,y5=0,z5=0;
reg [16:0] x6=0,y6=0,z6=0;
reg [16:0] x7=0,y7=0,z7=0;
reg [16:0] x8=0,y8=0,z8=0;
reg [16:0] x9=0,y9=0,z9=0;
reg [16:0] x10=0,y10=0,z10=0;
reg [16:0] x11=0,y11=0,z11=0;
reg [16:0] x12=0,y12=0,z12=0;
reg [16:0] x13=0,y13=0,z13=0;
reg [16:0] x14=0,y14=0,z14=0;
reg [16:0] x15=0,y15=0,z15=0;
reg [16:0] x16=0,y16=0,z16=0;

reg [1:0] quadrant [PIPELINE:0];
integer i;
initial
begin
    for(i=0;i<=PIPELINE;i=i+1)
    quadrant[i] = 2'b0;
end

//phase_in[15:14] determines which quadrant the angle is.
//00 means first;01 means second;00 means third;00 means fourth
//initialization: x0 = K,y0 = 0,z0 = phase_in,then the last result(x16,y16) = (cos(phase_in),sin(phase_in))  
always @ (posedge clk)//stage 0,not pipeline
begin
    x0 <= {1'b0,K}; //add one signed bit,0 means positive
    y0 <= 17'b0;
    z0 <= {3'b0,phase_in[13:0]};//control the phase_in to the range[0-Pi/2]
end
//pipeline
//z0[16] = 0,positive
always @ (posedge clk)//stage 1
begin
  if(z0[16])//the diff is negative so clockwise
  begin
      x1 <= x0 + y0;
      y1 <= y0 - x0;
      z1 <= z0 + `rot0;
  end
  else
  begin
      x1 <= x0 - y0;//x1 <= x0;
      y1 <= y0 + x0;//y1 <= x0;
      z1 <= z0 - `rot0;//reversal 45
  end
end
/*********************************************
//x(n+1） <= x(n) + {{n{y(n)[16]}},y(n)[16:n]}
**********************************************/
always @ (posedge clk)//stage 2
begin
    if(z1[16])//the diff is negative so clockwise
    begin
        x2 <= x1 + {y1[16],y1[16:1]};
        y2 <= y1 - {x1[16],x1[16:1]};
        z2 <= z1 + `rot1;//clockwise 26
    end
    else
    begin
        x2 <= x1 - {y1[16],y1[16:1]};
        y2 <= y1 + {x1[16],x1[16:1]};
        z2 <= z1 - `rot1;//anti-clockwise 26
    end
end

always @ (posedge clk)//stage 3
begin
    if(z2[16])//the diff is negative so clockwise
    begin
        x3 <= x2 + {{2{y2[16]}},y2[16:2]}; //right shift n bits,divide 2^n
        y3 <= y2 - {{2{x2[16]}},x2[16:2]}; //left adds n bits of MSB,in first quadrant x or y are positive,MSB =0 ？？
        z3 <= z2 + `rot2;//clockwise 14    //difference of positive and negtive number and no round(4,5)
    end
    else
    begin
        x3 <= x2 - {{2{y2[16]}},y2[16:2]};
        y3 <= y2 + {{2{x2[16]}},x2[16:2]};
        z3 <= z2 - `rot2;//anti-clockwise 14
    end
end

always @ (posedge clk)//stage 4
begin
    if(z3[16])
    begin
        x4 <= x3 + {{3{y3[16]}},y3[16:3]};
        y4 <= y3 - {{3{x3[16]}},x3[16:3]};
        z4 <= z3 + `rot3;//clockwise 7
    end
    else
    begin
        x4 <= x3 - {{3{y3[16]}},y3[16:3]};
        y4 <= y3 + {{3{x3[16]}},x3[16:3]};
        z4 <= z3 - `rot3;//anti-clockwise 7
    end
end

always @ (posedge clk)//stage 5
begin
    if(z4[16])
    begin
        x5 <= x4 + {{4{y4[16]}},y4[16:4]};
        y5 <= y4 - {{4{x4[16]}},x4[16:4]};
        z5 <= z4 + `rot4;//clockwise 3
    end
    else
    begin
        x5 <= x4 - {{4{y4[16]}},y4[16:4]};
        y5 <= y4 + {{4{x4[16]}},x4[16:4]};
        z5 <= z4 - `rot4;//anti-clockwise 3
    end
end

always @ (posedge clk)//STAGE 6
begin
    if(z5[16])
    begin
        x6 <= x5 + {{5{y5[16]}},y5[16:5]};
        y6 <= y5 - {{5{x5[16]}},x5[16:5]};
        z6 <= z5 + `rot5;//clockwise 1
    end
    else
    begin
        x6 <= x5 - {{5{y5[16]}},y5[16:5]};
        y6 <= y5 + {{5{x5[16]}},x5[16:5]};
        z6 <= z5 - `rot5;//anti-clockwise 1 
    end
end

always @ (posedge clk)//stage 7
begin
    if(z6[16])
    begin
        x7 <= x6 + {{6{y6[16]}},y6[16:6]};
        y7 <= y6 - {{6{x6[16]}},x6[16:6]};
        z7 <= z6 + `rot6;
    end
    else
    begin
        x7 <= x6 - {{6{y6[16]}},y6[16:6]};
        y7 <= y6 + {{6{x6[16]}},x6[16:6]};
        z7 <= z6 - `rot6;
    end
end

always @ (posedge clk)//stage 8
begin
    if(z7[16])
    begin
        x8 <= x7 + {{7{y7[16]}},y7[16:7]};
        y8 <= y7 - {{7{x7[16]}},x7[16:7]};
        z8 <= z7 + `rot7;
    end
    else
    begin
        x8 <= x7 - {{7{y7[16]}},y7[16:7]};
        y8 <= y7 + {{7{x7[16]}},x7[16:7]};
        z8 <= z7 - `rot7;
    end
end

always @ (posedge clk)//stage 9
begin
    if(z8[16])
    begin
        x9 <= x8 + {{8{y8[16]}},y8[16:8]};
        y9 <= y8 - {{8{x8[16]}},x8[16:8]};
        z9 <= z8 + `rot8;
    end
    else
    begin
        x9 <= x8 - {{8{y8[16]}},y8[16:8]};
        y9 <= y8 + {{8{x8[16]}},x8[16:8]};
        z9 <= z8 - `rot8;
    end
end

always @ (posedge clk)//stage 10
begin
    if(z9[16])
    begin
        x10 <= x9 + {{9{y9[16]}},y9[16:9]};
        y10 <= y9 - {{9{x9[16]}},x9[16:9]};
        z10 <= z9 + `rot9;
    end
    else
    begin
        x10 <= x9 - {{9{y9[16]}},y9[16:9]};
        y10 <= y9 + {{9{x9[16]}},x9[16:9]};
        z10 <= z9 - `rot9;
    end
end

always @ (posedge clk)//stage 11
begin
    if(z10[16])
    begin
        x11 <= x10 + {{10{y10[16]}},y10[16:10]};
        y11 <= y10 - {{10{x10[16]}},x10[16:10]};
        z11 <= z10 + `rot10;//clockwise 3
    end
    else
    begin
        x11 <= x10 - {{10{y10[16]}},y10[16:10]};
        y11 <= y10 + {{10{x10[16]}},x10[16:10]};
        z11 <= z10 - `rot10;//anti-clockwise 3
    end
end

always @ (posedge clk)//STAGE 12
begin
    if(z11[16])
    begin
        x12 <= x11 + {{11{y11[16]}},y11[16:11]};
        y12 <= y11 - {{11{x11[16]}},x11[16:11]};
        z12 <= z11 + `rot11;//clockwise 1
    end
    else
    begin
        x12 <= x11 - {{11{y11[16]}},y11[16:11]};
        y12 <= y11 + {{11{x11[16]}},x11[16:11]};
        z12 <= z11 - `rot11;//anti-clockwise 1 
    end
end

always @ (posedge clk)//stage 13
begin
    if(z12[16])
    begin
        x13 <= x12 + {{12{y12[16]}},y12[16:12]};
        y13 <= y12 - {{12{x12[16]}},x12[16:12]};
        z13 <= z12 + `rot12;
    end
    else
    begin
        x13 <= x12 - {{12{y12[16]}},y12[16:12]};
        y13 <= y12 + {{12{x12[16]}},x12[16:12]};
        z13 <= z12 - `rot12;
    end
end

always @ (posedge clk)//stage 14
begin
    if(z13[16])
    begin
        x14 <= x13 + {{13{y13[16]}},y13[16:13]};
        y14 <= y13 - {{13{x13[16]}},x13[16:13]};
        z14 <= z13 + `rot13;
    end
    else
    begin
        x14 <= x13 - {{13{y13[16]}},y13[16:13]};
        y14 <= y13 + {{13{x13[16]}},x13[16:13]};
        z14 <= z13 - `rot13;
    end
end

always @ (posedge clk)//stage 15
begin
    if(z14[16])
    begin
        x15 <= x14 + {{14{y14[16]}},y14[16:14]};
        y15 <= y14 - {{14{x14[16]}},x14[16:14]};
        z15 <= z14 + `rot14;
    end
    else
    begin
        x15 <= x14 - {{14{y14[16]}},y14[16:14]};
        y15 <= y14 + {{14{x14[16]}},x14[16:14]};
        z15 <= z14 - `rot14;
    end
end

always @ (posedge clk)//stage 16
begin
    if(z15[16])
    begin
        x16 <= x15 + {{15{y15[16]}},y15[16:15]};
        y16 <= y15 - {{15{x15[16]}},x15[16:15]};
        z16 <= z15 + `rot15;
    end
    else
    begin
        x16 <= x15 - {{15{y15[16]}},y15[16:15]};
        y16 <= y15 + {{15{x15[16]}},x15[16:15]};
        z16 <= z15 - `rot15;
    end
end
//according to the pipeline,register phase_in[15:14]
always @ (posedge clk)
begin
  quadrant[0] <= phase_in[15:14];
  quadrant[1] <= quadrant[0];
  quadrant[2] <= quadrant[1];
  quadrant[3] <= quadrant[2];
  quadrant[4] <= quadrant[3];
  quadrant[5] <= quadrant[4];
  quadrant[6] <= quadrant[5];
  quadrant[7] <= quadrant[6];
  quadrant[8] <= quadrant[7];
  quadrant[9] <= quadrant[8];
  quadrant[10] <= quadrant[9];
  quadrant[11] <= quadrant[10];
  quadrant[12] <= quadrant[11];
  quadrant[13] <= quadrant[12];
  quadrant[14] <= quadrant[13];
  quadrant[15] <= quadrant[14];
  quadrant[16] <= quadrant[15];
end
//alter register, according to quadrant[16] to transform the result to the right result
always @ (posedge clk) begin
eps <= z15;
case(quadrant[16]) //or 15
2'b00:begin //if the phase is in first quadrant,the sin(X)=sin(A),cos(X)=cos(A)
        cos <= x16;
        sin <= y16;
        end
2'b01:begin //if the phase is in second quadrant,the sin(X)=sin(A+90)=cosA,cos(X)=cos(A+90)=-sinA
        cos <= ~(y16) + 1'b1;//-sin
        sin <= x16;//cos
        end
2'b10:begin //if the phase is in third quadrant,the sin(X)=sin(A+180)=-sinA,cos(X)=cos(A+180)=-cosA
        cos <= ~(x16) + 1'b1;//-cos
        sin <= ~(y16) + 1'b1;//-sin
        end
2'b11:begin //if the phase is in forth quadrant,the sin(X)=sin(A+270)=-cosA,cos(X)=cos(A+270)=sinA
        cos <= y16;//sin
        sin <= ~(x16) + 1'b1;//-cos
        end
endcase
end

endmodule

`timescale 1 ns/ 1 ps
module cordic_vlg_tst();

reg clk;
reg [15:0] phase_in;
// wires                                               
wire [16:0]  cos;
wire [16:0]  eps;
wire [16:0]  sin;

localparam coef=1000;

// assign statements (if any)                          
cordic i1 (
// port map - connection between master ports and signals/registers   
	.clk(clk),
	.cos(cos),
	.eps(eps),
	.phase_in(phase_in),
	.sin(sin)
);
initial                                                
begin                                                  
   clk=0;
	phase_in=0;  
	#100000 $stop;  
end                                                    
always #10 clk=~clk;   
// phase_in[16:15]   
// 2'b00:  //if the phase is in first quadrant,the sin(X)=sin(A),cos(X)=cos(A)
// 2'b01:  //if the phase is in second quadrant,the sin(X)=sin(A+90)=cosA,cos(X)=cos(A+90)=-sinA
// 2'b10:  //if the phase is in third quadrant,the sin(X)=sin(A+180)=-sinA,cos(X)=cos(A+180)=-cosA
// 2'b11:  //if the phase is in forth quadrant,the sin(X)=sin(A+270)=-cosA,cos(X)=cos(A+270)=sinA                                             
always @(negedge clk)
begin                                                  
// phase_in=16'b10_11_1111_1111_1111;                   
  phase_in=phase_in + 8'b1000_0000;                                          
end                 
//0____90
//0____1
//0____65536

endmodule