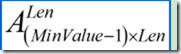前段时间做拓展训练，玩了一个游戏，名叫效益解码（也叫超音速）扑克游戏。

1 游戏规则

相互竞争的若干团队（每个团队10多个人），每个团队玩一副扑克牌，扑克牌包含1，2，3，…，J，Q，K共13张，扣在离团队5米之外的桌上，背面朝上，牌之间的顺序打乱，但是放牌的位置是有一定形状的，比如竖着放或者横着放（至于为什么需要这样，下一节的游戏策略会有解释）。团队成员需依次跑过去翻牌，必须按照由小到大的顺序翻开扑克牌。如果所翻的牌的顺序不符，则扑克牌必须被重新扣过来，然后成员返回，队伍继续让其他成员翻牌。最终哪队最先按顺序翻牌成功，哪队获胜。

2 游戏策略

当然不能凭运气。一个团队中，每个人都应该被分配去翻固定位置的牌，然后记住这个位置对应的点数（这里，上节的游戏规则中的位置有一定的形状就尤其重要了，如果位置随意，比如13张牌就随便扔为一堆，那么团队成员是不可能分辨出自己应该翻哪一张的）。当所有的牌都被翻过了之后，团队已经掌握了所有牌的位置信息。接下来要做的就是：如果需要翻几点，那个在之前翻过这张牌的人就马上冲过去把对应的牌翻过来。注意：当碰巧翻对牌之后，一定要让团队成员知道，否则大家都不知道下一个该翻什么牌。

从这里已经知道，最好的情况是第一个人恰好翻到1，第二个人恰好翻到2……最后一个人把最后一张K翻出来，一共只需翻13次。而最坏的情况是，前面12个人都没翻到1，第13个人翻到1了，然后剩下的12张牌就可以按照顺序翻出来了，一共需要25次。即完成游戏需要的次数分布在[13, 25]的整数区间，现在浮出2个问题：

• 若不限定时间，完成游戏需要的平均次数（即期望）是多少呢？
• 若限定时间（因为每个人来回的时间可以设为一个固定的常数，即等同于限制了翻牌的次数），则团队有多大的概率能够翻开所有牌？

3 每种次数的概率

按照期望的定义，需要先求得每种翻牌次数的概率。概率问题又可转化为如下的排列组合问题。只要我们计算出每种翻牌次数的可能的排列情况，便可知道该次数在总的次数分布中所占的比例，进而求得期望。进而上述的2个问题都可解决。

该问题可转化为：有1到13共13个数。取出2到13中的某些数，插入到这个数列中，插入的要求是：对于每一个插入进去的数，其数值必须比右边的相邻的数要大。例如，若要求翻牌次数为14次的可能排列的情况，就要从“2”到“13”中选一个数，插入到该数列中。如果选的是“3”，则只能插到“1”或者“2”的前面，只有2种可能，如下图所示。

若要求翻牌次数为15次的可能排列的情况，就要从“2”到“13”中选2个数，插入到该数列中，如下图所示。如果选的是“3”、“4”。则这2个数全都只能插到“1”或者“2”的前面。因为虽然“4”比“3”大，但不可能出现1、3、2、4、3、4、5、…12、13这种情况，因为如果第2次翻的“3”（此时要求翻2，不符合要求，牌又会被扣回去），第3次翻的2，则第四次一定会把3翻出来，因为已经知道“3”的具体位置了，不可能再去翻其他不符合要求的牌，白白浪费一次时间。

……以此类推。

所以，若选出了一组数，这些数全都只能插入到最小值的左边相邻的牌的左边。比如上面的“3”和“4”，只能插到“2”的左边。

所以，对于某一组选出来的特定的数，其能够插入到的位置的可能排列次数为

其中MinValue为这一组数的最小值，Len为这组数的个数。

所以，问题的关键就是，对于需要选出的特定个数的牌，如何从2到23中遍历组合。比如，需要从2到13中选3个数，如何遍历这3个数的所有组合？咱们用深度优先搜索（Deep First Search， DFS）来实现遍历。当然，实现DFS所需要的数据结构就是栈。

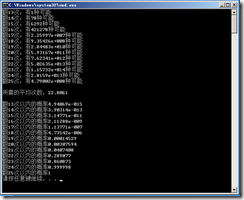
C++代码在最后，整个游戏需要的次数的期望为22.8次，并不像我们直观的猜测那样，是最小次数13次和最大次数25次的平均。详细结果如下图

4 算法优化

既然我们知道，对于一个特定的组合，其排列次数只和最小值有关，那么我们是不用遍历所有组合的，只需要计算出最小值为2,3，……的组合的次数，再计算出对应的排列次数，两者相乘，就可以得到取出固定个数的排列次数了。今天写累了，过几天再写个续吧。

附件：代码。。。

微盘也上传了一份：Poker_Method1

#include

#include

#include

#define FLIP_CNT 13 // 牌的数目

using namespace std;

bool AccessFlag[FLIP_CNT - 1]; // 对应节点是否被访问，若被访问，置为1，若没被访问，置为0，其中AccessFlag[i]对应于数字i+1

int getCombCnt(int n, int k) // 求组合C(n, k)的个数

{

__int64 PermutationCnt; // C(n,k)对应的排列次数A(n,k)

__int64 Factorial; // 阶乘: k!

__int64 CombCnt; // 需要返回的组合次数C(n,k)

__int64 Temp, i;

if ( k == 0 || k == n )

return (1);

else

{

if ( k > n/2 ) // 组合有个恒等式：C(n,k) = C(n,n-k)

k = n - k;

PermutationCnt = 1;

Factorial = 1;

Temp = (__int64)n;

for ( i = 0; i < k; i ++ )

{

PermutationCnt = PermutationCnt * Temp;

Factorial = Factorial * (i + 1);

Temp --;

}

CombCnt = PermutationCnt / Factorial;

return ((int)CombCnt);

}

}

vector getNewCombination(vector LastCombination) // 针对当前的组合，算出下一个组合

{

vector NewCombination; // 需要返回的新的组合

int Len, Addr, CurrentLen;

int i, j;

Len = LastCombination.size(); // 当前组合的个数，用以限制入栈的个数

CurrentLen = Len;

Addr = LastCombination[Len - 1] + 1; // 下一个访问的地址=当前pop出的地址+1

LastCombination.pop_back();

CurrentLen --;

for ( j = Addr; j <= FLIP_CNT-2; j ++ ) // 长度为FLIP_CNT-1，当然地址最高为FLIP_CNT-2

AccessFlag[j] = 0;

while ( LastCombination.size() != Len )

{

for ( i = Addr; i <= FLIP_CNT-2; i ++ )

{

if ( AccessFlag[i] == 0 ) // 如果当前节点没被访问，入栈

{

LastCombination.push_back(i);

AccessFlag[i] = 1;

CurrentLen ++;

}

if ( LastCombination.size() == Len )

break; // 跳出for循环的话也肯定会跳出外面一层的while循环

}

if ( i == FLIP_CNT-1 ) 

{

Addr = LastCombination[CurrentLen - 1] + 1; // 要从当前pop的地址之后的AccessFlag全部复位为0

LastCombination.pop_back();

CurrentLen --;

for ( j = Addr; j <= FLIP_CNT-2; j ++ )

AccessFlag[j] = 0;

}

}

NewCombination = LastCombination;

return(NewCombination);

}

double getPermutationCnt(vector Combination) // 计算当前组合对应的排列次数

{

int Len, i;

double PermutationCnt = 1.0;

double Temp, MinValue;

Len = Combination.size();

MinValue = Combination[0]; // 根据入栈和出栈的规则，栈底的值为最小值

Temp = double((MinValue + 1) * Len);

for ( i = 0; i < Len; i ++ )

{

PermutationCnt = PermutationCnt * Temp;

Temp --;

}

return (PermutationCnt);

}

int main()

{

int CombCnt[FLIP_CNT]; // 每种选取数目对应的组合个数

double Cnt[FLIP_CNT]; // 每种翻牌次数对应的可能次数

double PermutationCnt; // 针对每种取出的组合，计算其排列次数

int i, j, Addr;

double AccumulatedCnt[FLIP_CNT]; // 累积分布次数

double AccumulatedProb[FLIP_CNT]; // 累积分布概率

double Temp; // 只是为了求所需次数的期望的一个中间值

double MeanCnt; // 所需次数的期望

vector Comb, NewComb; // 取出的数的组合

memset(Cnt, sizeof(Cnt), 0);

memset(Cnt, sizeof(AccessFlag), 0);

for ( i = 0; i < FLIP_CNT; i ++ ) // 从C(FLIP_CNT-1,0)到C(FLIP_CNT-1,FLIP_CNT-1)

CombCnt[i] = getCombCnt(FLIP_CNT - 1, i);

Cnt[0] = 1;

cout << "翻" << FLIP_CNT << "次：有1种可能" << endl;

for ( i = 1; i < FLIP_CNT; i ++ ) // i表示选中的个数，可能值为1~25

{

Comb.clear();

for ( Addr = 0; Addr < i; Addr ++ ) // 入栈初始化

{

Comb.push_back(Addr); // 为了节省内存，直接把地址入栈，真实的点数是Addr+2

AccessFlag[Addr] = 1; // 入栈之后，AccessFlag置1

}

Cnt[i] = getPermutationCnt(Comb); // 计算当前组合对应的排列次数

for ( j = 1; j < CombCnt[i]; j ++ ) // 针对每种组合的数目，从1开始，因为在for循环前已经计算过一次了

{

NewComb = getNewCombination(Comb); // 遍历组合

PermutationCnt = getPermutationCnt(NewComb); // 针对当前的选出的组合，插入到牌中，需要计算排列的数目

Cnt[i] = Cnt[i] + PermutationCnt;

Comb = NewComb;

}

cout << "翻" << i + FLIP_CNT << "次：有" << Cnt[i] << "种可能" << endl;

}

cout << endl;

AccumulatedCnt[0] = 1.0;

Temp = FLIP_CNT * 1.0;

for ( i = 1; i < FLIP_CNT; i ++ )

{

Temp = Temp + (i + FLIP_CNT) * Cnt[i];

AccumulatedCnt[i] = AccumulatedCnt[i - 1] + Cnt[i];

}

MeanCnt = Temp / AccumulatedCnt[FLIP_CNT-1]; // 所需次数的期望

for ( i = 0; i < FLIP_CNT; i ++ )

AccumulatedProb[i] = AccumulatedCnt[i] / AccumulatedCnt[FLIP_CNT-1]; // 所需次数的累积分布概率

cout << "所需的平均次数：" << MeanCnt << endl << endl;

for ( i = 0; i < FLIP_CNT; i ++ )

cout << "翻" << i + FLIP_CNT << "次以内的概率" << AccumulatedProb[i] << endl;

return 0;

}