数值运算是MATLAB的核心功能。但广大科研人员对符号运算的需求催生MATLAB产生了一个新的工具箱：Symbolic Math Toolbox。

先来看一个简单的例子：

syms a b c x

f = a*x^2 + b*x + c;

便定义了一个符号函数f

如果要将f中的某些参数替换为数值，用subs函数

g = subs(f, {a, b, c}, {1, 4, 1});

表示将a替换为1，b替换为4，c替换为1。

除了syms类型，inline和匿名函数也是该Symbolic Math Toolbox的常客。

1 inline与匿名函数（Anonymous Functions）

利用inline函数生成inline object的简单例子如下：

f = inline('a*x^2 + b*x + c', 'a', 'b', 'c', 'x')

f(1, 2, 3, 1)

结果为：

f =

Inline function:

f(a,b,c,x) = a * x^2 + b * x + c

ans =

6

但MATLAB官方已经申明在后续的版本中inline会被移除，取而代之的是匿名函数（Anonymous Functions）。之所以有必要搞清楚这个新东西，是因为MATLAB提供的很多其它函数的argin只能为function handle，比如integral, fzero, and fminbnd函数。

将上述代码改为匿名函数的代码如下，而匿名函数的调用同普通子函数function一样，括号里面为输入参数

f = @(a, b, c, x) a*x^2 + b*x + c

f(1, 2, 3, 1)

结果为：

f = 

@(a,b,c,x)a*x^2+b*x+c

ans =

6

但是，如果argin中只要有一个不是数值，而是参数，要么在调用前用syms定义此参数，要么在调用的时候再以@开头，声明为匿名函数

f = @(a, b, c, x) a*x^2 + b*x + c

y1 = @(x) f(1, 2, 3, x)

syms x

y2 = f(1, 2, 3, x)

结果为：

y1 = 

@(x)f(1,2,3,x)

y2 =

x^2 + 2*x + 3

可以在workspace中看到y1为function handle，y2为syms，而在运行第三行：syms x之前，workspace中是不会有x的。这方面的技巧在后续的解方程时会用到，见3.2小节。

定义匿名函数时，如果不支持向量输入，那么调用的时候也不能将向量作为输入参数，否则报错：

f = @(x)x^2;

f([2 3])

会报错：

Error using  ^ 

Inputs must be a scalar and a square matrix.

To compute elementwise POWER, use POWER (.^) instead.

此时可以利用arrayfun函数解决该问题

f = @(x)x^2;

arrayfun(f,[2 3])

结果为：

ans =

4   9

所以，为了避免argin只能为scalar，最好在定义的时候就向量化

f = @(x)x.^2;

f([2 3])

结果为：

ans =

4   9

匿名函数有个很独特的性质：就算在workspace中clear掉匿名函数需要用到的变量，再次调用该函数时也不会报错。

k = 3;

f = @(x) k * x;

f(2)

clear k

f(3)

运行结果如下：

ans =

6

ans =

9

2 积分函数int & integral & quad

int是Symbolic Math Toolbox的，而integral和quad属于MATLAB通用工具箱

2.1 不定积分

符号积分有个数值积分没有的功能：不定积分。显然，定积分算出来本身就是一个数，当然没有不定积分这一说法。

int(1/x)

结果：

ans =

log(x)

2.2 定积分

2.2.1 int

用int积分的代码如下：

syms x;

y1 = int(1/x, 1, 2);

yy1 = eval_r(y1)

结果：

yy1 =

0.6931

由于int是符号工具箱的，就算定积分算出来是数值，其类型也是syms，要eval一下。另外，int函数的第一个argin必须为syms类型，字符串、inline或者function handle都不行，以下3种调用方式全错

y2 = int('1/x', 1, 2);

y3 = int(inline(1/x), 1, 2);

y4 = int(@(x) 1/x, 1, 2);

结果：

Undefined function 'int' for input arguments of type 'char'.

Undefined function 'int' for input arguments of type 'inline'.

Undefined function 'int' for input arguments of type 'function_handle'.

2.2.2 integral & quad

MATLAB官方已经申明在后续的版本中quad会被移除，取而代之的是integral函数。不过鉴于quad函数仍被大家所熟悉，本文还是简要介绍一下quad。

• quad函数的第一个输入参数fun，可以为字符串或者inline函数或者function handle
• integral函数的fun只能为function handle

f1 = '1./x.^2';

f2 = inline('1./x.^2');

f3 = @(x) 1 ./ x.^2;

quad(f1, 1, inf)

quad(f2, 1, inf)

quad(f3, 1, inf)

integral(f1, 1, inf)

integral(f2, 1, inf)

integral(f3, 1, inf)

会报错：

Error using integral (line 82)

First input argument must be a function handle.

另外，注意这2个函数都要求fun为向量化函数！如果定义的时候忘了向量化了，用vectorize(fun)

3 解方程solve & fzero

solve可以求符号解和数值解，而fzero只能求数值解，而且fzero必须至少2个argin，第一个为fun，第二个为指明在某个值的附近搜索根。具体参见Help。

3.1 solve

solve不仅可以求出具体的一元方程的根，还可以求出符号表达式，但此时必须指明是针对哪个变量，而且solve的第一个argin eqn可以为符号表达式，也可以为function handle，但不能为inline。如下2种方式得到相同的结果，

f = @(a, b, c, x) a*x^2 + b*x + c;

x1 = solve(f, 'x')

x2 = solve(f, 'a')

syms a b c x;

g = a*x^2 + b*x + c;

x3 = solve(g, 'x')

结果：

x1 =

-(b + (b^2 - 4*a*c)^(1/2))/(2*a)

-(b - (b^2 - 4*a*c)^(1/2))/(2*a)

x2 =

-(c + b*x)/x^2

x3 =

-(b + (b^2 - 4*a*c)^(1/2))/(2*a)

-(b - (b^2 - 4*a*c)^(1/2))/(2*a)

可以看到，虽然f和g的类型不同，但解方程得到的x1和x3都是syms类型。如果用inline，会报错

q = inline('a*x^2 + b*x + c');

x3 = solve(q, 'x')

Error using sym>tomupad (line 1135)

Conversion to 'sym' from 'inline' is not possible.

Error in sym (line 151)

S.s = tomupad(x);

Error in solve>getEqns (line 410)

a = formula(sym(a));

Error in solve (line 227)

[eqns,vars,options] = getEqns(varargin{:});

Error in Untitled2 (line 27)

x3 = solve(q, 'x')

3.2 fzero

求x^2 + 4*x + 1=0的根。可以看到，fzero对function handle和inline和string都支持，但其Help中没有指明函数类型的要求，只有自己试了

f1 = @(a, b, c, x) a*x^2 + b*x + c;

x1 = fzero(@(x) f(1, 4, 1, x), -2 - sqrt(3))

f2 = inline('1*x^2 + 4*x + 1');

x2 = fzero(f2, -2 - sqrt(3))

x3 = fzero('1*x^2 + 4*x + 1', -2 - sqrt(3))

运行结果为

x1 =

-3.7321

x2 =

-3.7321

x3 =

-3.7321

注意：上面第二行不能去掉@(x)，否则会报错：

Undefined function or variable 'x'.

具体原因可以参考第1节匿名函数的调用。

但是fzero不支持syms类型的函数，如下的代码会报错

syms a b c x;

f4 = a*x^2 + b*x + c;

f4 = subs(f4, {a, b, c}, {1, 4, 1});

x4 = fzero(f4, -2 - sqrt(3))

报错信息：

Error using fzero (line 169)

If FUN is a MATLAB object, it must have an feval method.

Error in Untitled2 (line 71)

x4 = fzero(f4, -2 - sqrt(3))

Error using fzero (line 128)

FZERO accepts inputs only of data type double.

4 syms类型的函数转换为function handle：str2func

syms a b c x;

g = a*x^2 + b*x + c;

f1 = str2func(['@(x)', char(g)])

f2 = str2func(['@(x)', vectorize(char(g))])

char函数表示将syms类型的g转换为字符串类型，再调用str2func就可以了。之所以f2在char之后还vectorize了，是便于后续调用integral或者quad函数。

与str2func相反的函数是：func2str

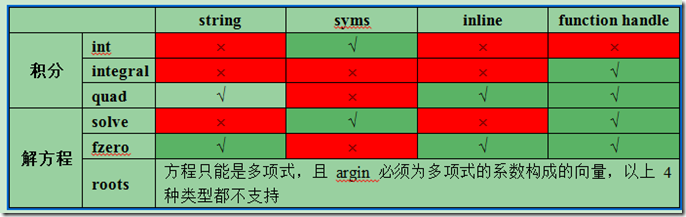
5 各个函数对argin中fun的类型要求总结