基于启发式阈值(heursure)的小波变换去噪方法
0赞4、基于启发式阈值(heursure)的小波变换去噪方法
通过上文介绍的三种小波滤波方法,本文采用阈值去噪和去除低频逼近信号相结合的方法实现心电信号的滤波。该算法利用小波的多分辨率特性,首先通过Mallat算法对ECG信号进行多尺度分解,观察不同尺度下细节信号和逼近信号的特点,在分解的各个尺度上用启发式小波阈值(heursure)函数方法对小波系数进行处理,然后用各尺度上的估计小波系数重构原始信号,最后去除近似于基线漂移干扰的逼近信号的重构信号。小波变换去噪框图如图所示:

|
|
4.1 小波基函数的确定
波基函数的选取对信号去噪的效果起到至关重要的作用。通过上文几种小波基函数的介绍,我们可以知道db系列小波、bior系列小波、sym系列小波及coif系列小波都可以对心电信号进行分解和重构。现在我们利用启发式小波阈值函数形式,分别采用这几种典型的小波对同一段心电信号进行4个尺度下的分解与重构,实验结果如下图所示:

|

|
|


|

|
通过以上理论分析和实验,我们可以看出coif5小波的去噪效果要优于db4、bior3.5和sym8小波。本文采用小波变换中的第二代整型coif5小波进行ECG,信号的分解与重构,其核心原理是利用小波变换的多尺度特性。
4.2 分解尺度的确定
分解尺度也是影响信号去噪效果的一个重要因素。随着小波分解尺度的增力口,逼近信号中的高频信息会越来越少,剩下的部分就逐渐接近基线漂移的分量。这就是利用低频逼近信号滤除基线漂移干扰的原理所在。因此分解尺度的确定依赖于能够反映基线漂移干扰的逼近信号所在的尺度。然而分解尺度也不是越多越好,尺度越多计算量也就越大,因此合理的确定分解尺度很关键。
我们用coif5小波函数对MIT-BIH数据库中—段含有基线漂移干扰的数据进行4、 6、 8、 10、 12尺度下的分解,各个尺度下的逼近信号的重构波形如图所示:

|
||||
|
||||
|
||||


|


|
|

由上图可以看出,对ECG信号进行分解时,若分解尺度较小(如a4、a6),得到的逼近信号中含有较多的高频成分,通过去噪处理后会损失信号中的有用分量;若分解尺度较大(如a12),逼近信号则不能充分地反映基线漂移的信息,也就无法通过处理低频逼近信号来有效地抑制基线漂移干扰。通过多组数据实验,本文最终确定分解尺度为10时,噪声干扰的抑制效果最好。
4.3 ECG信号中噪声干扰的滤除
心电信号滤除的干扰主要有三种:工频干扰、肌电干扰及基线漂移。本文采用不同的滤波方法实现三种干扰的抑制。基于启发式小波阈值(heursure)函数方法主要去除ECG信号中的工频干扰和肌电干扰;ECG信号中基线漂移的滤除我们通过减去低频逼近信号的重构信号的方式来实现。
基于改进阈值的小波去噪算法主要步骤如下:
第一步:确定小波基函数和分解尺度。采用coif5小波函数将原始心电信号f(t)进行10个尺度下的分解;
第二步:对1到4尺度上的小波系数利用启发式小波阈值(heursure)函数方法,实现各个尺度上的滤波处理,去除ECG信号中的工频干扰和肌电干扰;
第三步:分解得到第10个尺度上的逼近信号a10(n),将细节d1(n)、d2(n)、···、d10(n)的系数全部置零,再和a10(n)一起做小波反变换,得到a10(n)的重构信号。
第四步:将a4(n)的重构信号减去a10(n)的重构信号,得到滤除噪声后的心电波形。
4.4 实验结果分析
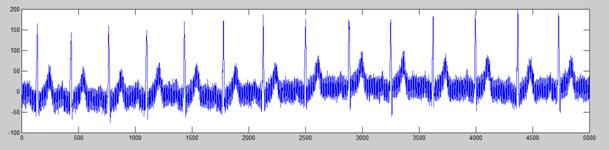
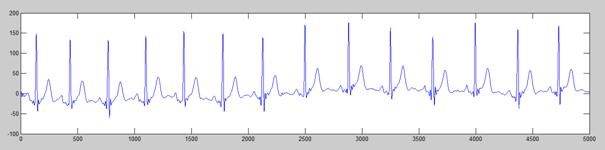
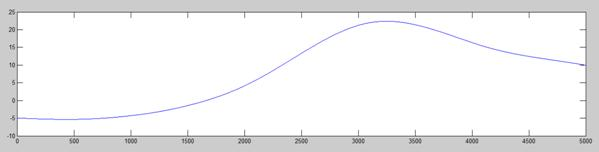
为了验证基于启发式阈值(heursure)的小波变换去噪方法的性能,本文选取MIT-BIH数据库中一段含有基线漂移的心电信号数据进行去噪处理,结果如下图所示:
|
|
|
|
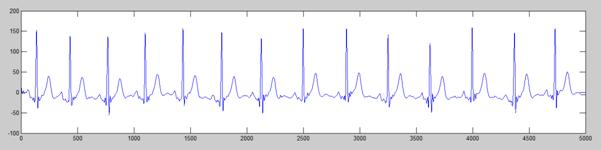
由实验结果可以看出,原始心电波形含有一定的基线漂移和高频噪声,对原始信号利用启发式小波阈值(heursure)函数方法进行滤波后,滤除了大部分的高频噪声,但是基线漂移并没有消除,如图4.4.2所示。对原始信号进行10个尺度的分解,得到低频逼近信号a10(n),对a10(n)进行重构后就可以得到基线漂移信号,如图4.4.3所示。最后将a4(n)重构信号减去基线漂移信号,得到滤除噪声后的心电信号,如图4.4.4所示。由上图可以看出,经过去噪处理后的心电信号(图4.4.4)相比原始心电信号(图4.4.1)更加接近人体的心电信号,基线漂移噪声得到了较好的抑制,QRS波群的特征也更加明显。但是仔细观察,可以看到在Q波和S波附近还是存在一些较明显的噪声,有待进一步的改进。
