分布式算法（Distributed Arithmetic，DA）是一种专门针对乘加运算而优化的运算方法。与传统算法相比，分布式算法可以极大地减少硬件电路规模，很容易实现流水线处理，提高电路的执行速度。而这正是很多数字系统所极力追求的目标，正所谓“鱼与熊掌有的时候也可以兼得也！”。

所谓分布式算法，就是指在完成乘加功能时通过将各个输入数据每一位对应产生的运算结果预先进行相加形成相应的部分积，然后再对各部分积进行累加，以获得最终的计算结果。而传统的算法则是等到所有的乘积结果产生之后再进行相加的，然后产能完成最终的乘加运算。

需要特别说明的是，分布式算法有一个前提条件：每个乘法运算中必须有一个乘数为常数。熟悉FIR滤波器的朋友应该知道，FIR滤波器的基本结构正是这样的乘加运算。因此，分布式算法在FIR滤波器设计中有着广泛的应用，采用分布式算法，甚至可以在那些没有DSP资源的低端FPGA或者CPLD中完成FIR滤波器设计。

那么，如何来理解分布式算法呢？还是先从最基本的固定系数乘法运算说起。对于一个乘数是常数的乘法运算来说，很容采用ROM来完成乘法运算，将变量作为ROM地址输入，结果预先存放在ROM中。而读取ROM操作所消耗的时间要比乘法运算少很多（即使是基于DSP的乘法运算），并且消耗的资源也更少。

注：实际上，所有乘除常数的定点数运算，都可以采用将乘除法转换为加减和移位运算（例如A÷5可以转换为A×（0.125+0.0625+0.0156）），具体可以参考：http://blog.chinaaet.com/justlxy/p/5100059794。相比于分布式算法，这种方法消耗的资源更少，性能也还不错。分布式算法的优势在于对于那种大规模乘加运算，更容易优化为多级流水线结构。

因此，变量乘以常数可以采用对ROM进行寻址来实现，而这很容易用查找表来实现。对于FPGA来说，最不缺的就是查找表了，因此这种方式很适合在FPGA上面进行实现。用FPGA实现分布式算法的基本思想就是使用查找表结构（ROM寻址）来实现乘加运算，关键的问题是如何将乘加运算转换为可以采用查找表方法实现的结构形式。

以无符号数为例：

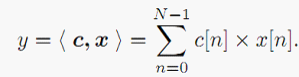
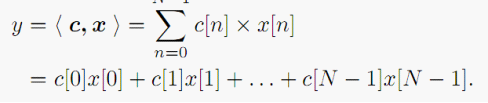
将X[n]看为变量，并按二进制分解表示（假设位宽为B）：

将X项展开并重新排列，并将C项展开

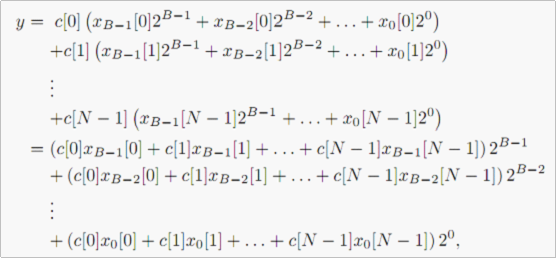
所谓的重新排序其实可看为是矩阵运算。刚开始出现一个矩阵：竖方向为第n次抽样递增 横方向为第b位递减。把两个矩阵相乘转换为3个矩阵相乘，其中有矩阵倒置操作。每一次n次抽样中得到的的第b位分别于C的第n位相乘

进一步表示为：

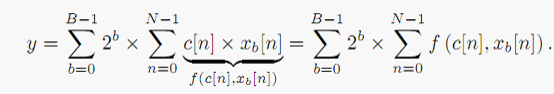
系统的结构框图如下，图中a为传统算法，b为分布式DA算法。

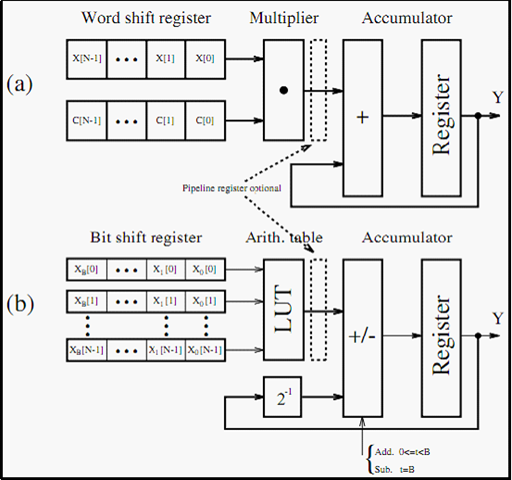
最后，再举一个具体的例子：

主要参考文献：

【1】网友ALIFPGA的博客：https://blog.csdn.net/woshifennu1234/article/details/80852182

【2】网友清风醉明月 slp_art的博客：

https://www.cnblogs.com/sleepy/archive/2011/07/25/2116657.html

【3】王勇. 数字滤波器的MATLAB与FPGA实现. 2017版