0 引  言

    在微波平面电路研究领域中，微带线是一种最重要的平面传输线，它以剖面薄、体积小、重量轻、使用频带宽、可靠性高、制造成本低、易于集成等特点得到广泛应用^[1-4]。在实际微带电路设计中，由于体积空间的限制，一些微波固态器件，在实际应用中，常常会遇到微带线拐弯、T 形分支、截断或隙缝等不连续性结构。这些不连续性将使微带电路参量发生变化，从而影响电路的性能^[5]。特性阻抗是射频与微波电路传输线中非常重要的一个参量。在微带线的拐弯处，由于宽度的变化，往往导致了寄生电抗的存在。相对于理想的直微带线，这种弯曲的结构就存在阻抗匹配问题^[6]。四分之一波长阻抗变换对于两端口阻抗值差异明显的情况下才适用，这时需要对微带线拐弯处进行适当处理，通过不同切削方式进行补偿，并利用业界比较权威的无源电磁仿真软件Ansoft HFSS进行仿真和优化，通过比较,得到了微带线直角拐弯的不连续性情况的最佳补偿方式。

1 微带线结构

    常见微带线结构如下图1所示。它是由接地板、厚度为h介电常数为εr的介质基片、长为L宽为W厚度为t的导体构成。其通常采用薄膜工艺制成。介质基片要求是介电常数高、微波损耗低、导热性好的材料^[7]，常选用氧化铝、石英、砷化镓、Duroid5880等。对于导体，要求导电率高、稳定性好、与基片的粘附性强，通常选用廉价易得的铜。应用中，介质基片与金属导带共同对微波信号进行传输。

图1  微带线结构

2 微带线的分析设计

为了更好的分析微带线，引入了一个参数------有效介电常数ε_e，它可以解释为一个均匀媒质的介电常数^[8]，定义为：

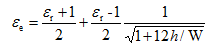            (1)

    如果已知微带线的尺寸，其特性阻抗Z₀可以计算为：

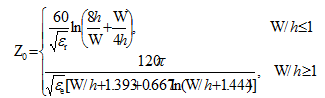 (2)    　　　　　　　　　　　　　　　　　　　 　　　　　　　　　

由此可知，对于任意微带线，已知导体宽度W、厚度h以及介质的介电常数ε_r，通过以上两式即可计算出其特性阻抗。

然而，实际的微带线设计时，往往遇到的是以上问题的逆问题。绝大多数情况下，所设计的微带电路要求与标准的50Ω阻抗相匹配。在不同的中心频率、相移、介质介电常数和介质厚度的情况下，微带线的尺寸是不同的。其比值W/h可求得为：

   (3)

　　其中，。

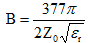如果已知微带线的相移角度Φ，则需要计算微带线的长度L，由于

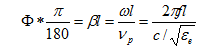        (4)

可得                          

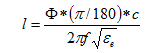     　       (5)

这里，c为微波在真空中的传播速度，即c=3.0×10⁸ m/s，β为传播常数，ν_p为相速。可见，特性阻抗与微带线的长度无关。故在设计微带电路时，如果已知工作中心频率、相移角度、介质厚度和介质的介电常数即可通过（1）、（3）、（5）式求得微带线尺寸。

然而，上面的公式略显复杂，计算起来比较麻烦。随着人们对微带线研究的进一步深入，微带线的计算工具逐渐被人们所使用。常见的有安捷伦（Aligent）公司的先进设计系统（Advanced Design System，ADS）软件中自带的工具，用户可根据不同的设计指标要求，能很快得到所需要的设计数据。其界面如下图所示：

图2  ADS中LineCalc 工具界面

也可以使用AWR公司的TXLINE软件，其中包含了微带线、共面波导、同轴线等多种传输线结构尺寸的计算。可根据不同的设计指标要求，很快得到所需要的设计数据。其界面如下所示：

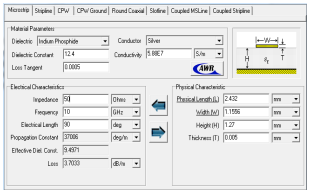
图3  TXLINE软件界面

    相比较而言，两者都可在不同传输线进行正向或逆向计算且能快速地获得微带线尺寸，从而为设计者提供了方便。不同的是，LineCalc工具较Txline软件具有所能计算的传输线类型较多、与真实计算值相比结果更加精确等优点。

3 微带线的不连续性结构及其分析

常见的微带线不连续性结构的典型表现是：微带线弯折、宽度上的阶梯变化、同轴-微带过渡、T 形分支、隙缝、开端微带等结构。研究发现，由微带线不连续性引起的的辐射损耗也是不容忽视的^[9]。在微带拐角处，容易导致寄生电抗的存在，并且带有杂散场和高阶模，从而使微带电路参量发生变化，影响电路的性能，因此很有必要消除由于微带拐角对其传输特性的不利影响。

文献[8]对微带线不连续性进行了简要分析，并介绍了常见两种补偿方法，使得电路不连续性效应最小。为进一步研究提供了思路。文献[5]研究了微带线拐角边长a及扫掠补偿的半径r对S参数的影响。文献[10]分析了不同介电常数下的切削角与W/h（与微带导体宽度和介质厚度之比）变化的关系。文献[11]根据微带线不连续性补偿理论，利用Ansoft HFSS对两种补偿方式进行仿真，证明了研究结果的正确性和可参考性，并得出了直角切削a=1.6W（文献[8]中）和圆弧切削R=3W时仿真结果最优的结论。根据文献[8]的微带线不连续性补偿理论及绝大多数参数（仅有介质选取不同）用Ansoft HFSS软件对以上两种情况建立的模型如下图：

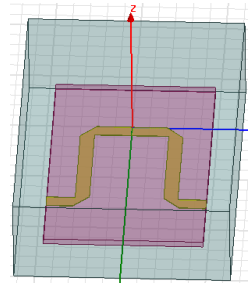
图4 直角切削模型（切边a=1.6W）

图5 圆弧切削模型（R=3W）

对以上建立的两个模型分别进行仿真，得到的端口传输系数及反射系数如下表所示：

表1 微带线拐弯处两种不同类型补偿方法的仿真结果（介质：Roger R04350  介电常数：εr=3.66）

     通过以上仿真结果与文献[11]比较，在相同频段、相同微带线特性阻抗和相同类型补偿结构、不同介质下的仿真结果，不难发现，无论是插入损耗还是回波损耗，仿真出来的效果大都比文献[8]中的效果要好。仅有R=3W的圆弧切削情况下，传输损耗相对于文献[11]略差。

进一步研究发现，在微带导体拐弯处内外圆弧切削皆为R=3W的情况下，微带线转弯处的线宽与非拐弯处的线宽并不相等，前者比后者偏大，当导体较宽的情况下，这种趋势更为显著。因此可以尝试一种寻求一种更好的补偿方式。

4 微带线拐弯外侧圆形扫掠补偿

4.1 定性分析

如图6所示，在微带线拐弯处内侧为圆心，对其外侧做一圆倒角，使得微带线在拐弯处的宽度都等于非拐弯处的宽度。在其他条件都不变的情况下，线宽的变化是其产生寄生电抗的唯一因素。将微带线拐弯处作以上处理，通过定性分析，在一定程度上能解决不连续性问题。

图6 微带线拐弯外侧圆形扫掠示意图

4.2 建模及仿真

为了证明以上分析的正确性， 选取了与上节相同介电常数的介质基片，通过前面的公式计算微带线的相关参数，并用软件对参数进行验证后，利用HFSS软件按照上述分析对微带线建立模型。相关参数设置为：特性阻抗均为50Ω，中心频率f₀=0.95GHz，扫频范围0.9GHz─1GHz。中心导带厚度T=0.02mm，介质厚度h=0.254mm，电长度为90度。建立的模型如下图7,模型建立后，对该模型进行仿真分析，得到的结果如下图8-图9。

图7 微带线拐弯外侧圆形扫掠模型

图8 微带线拐弯外侧圆形扫掠下的端口反射系数

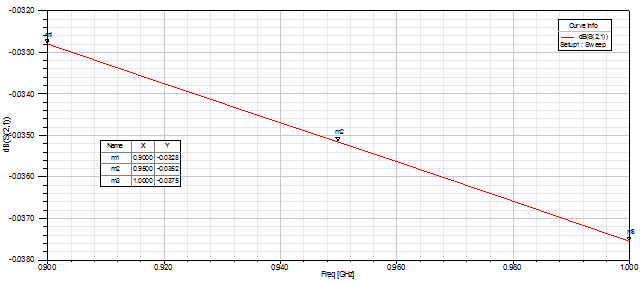
图9 微带线拐弯外侧圆形扫掠下的端口传输系数

由以上两图可以发现，微带线经过拐弯外侧圆形扫掠处理后的传输损耗非常小，在0.038dB以下。端口反射损耗极大，达43.7dB以上。这都说明端口反射回来的能量很小，从而使得几乎所有能量都能从一个端口传输到另一端口。

5 结  语

采用三种不同方式对微带线不连续性进行了补偿，利用电磁仿真软件Ansoft HFSS对微带线拐弯所产生的不连续性情况进行建模仿真分析。仿真结果表明，微带线拐弯外侧圆形扫掠的仿真结果为最佳。结合图7与表1，尽管a=1.6W与微带线拐弯外侧圆形扫掠两种不连续性补偿情况下的传输系数大致相当，但后者的端口反射系数大大优于前者，因而采用微带线拐弯外侧圆形扫掠的方法对微带线拐弯所产生的不连续性情况有更大的改善。

参考文献

[1]M.M.Radmanesh.射频与微波电子学[M].北京：科学出版社，2007；237-243.

[2]赵欢欢，姚爱琴，孙运强.一种新颖的双频微带天线设计[J].无线电通信技术，2016.42(2):63-65.

[3]李奇威，郭陈江，张兴华.平行耦合微带线带通滤波器的设计与优化[J].电子设计工程,2012.20 (4):12-14+18.

[4]王利萍，周东方，彭强等.基于拓扑网络的屏蔽腔体内置微带线响应分析[J].电波科学学报，2014.29(2):321-327.  

[5]陈鹏，曹沐昀.微带线不连续性补偿方法仿真研究[J].电子科技，2013；26(3).120-121.

[6]Reinhold Ludwig等.RF Circuit Design--Theory and Applications,Second Edition[M]. 北京:电子工业出版社，2013；287-291.

[7]清华大学微带电路编写组.微带电路[M].北京：人民邮电出版社，1976；4.

[8]David M.Pozar .Microwave Engineering.Third Edition[M].北京：电子工业出版社，2014；124

[9]毛剑波,黄正峰,杨明武,汪涛,宣晓峰.微带线不连续性辐射研究[J].电子测量与仪器学报，2012；26(5)：392-397.

[10]王克伟,王均宏.微带线拐角传输及反射特性研究[J]．微波学报，2006；22(3)：32-35．

[11]陈慰,赵娜,陶学敏. 微带线不连续性补偿方法的HFSS仿真分析[J]. 现代电子技术， 2001；34( 13) ：92-94.

蔡德龙（1991-）男，四川达州人，西南科技大学在读硕士研究生，主要研究方向：微波毫米波技术。联系方式：275703863@qq.com