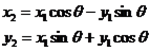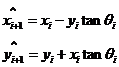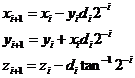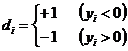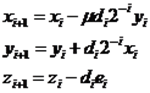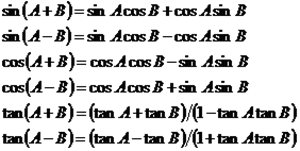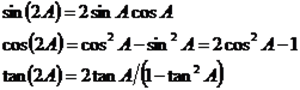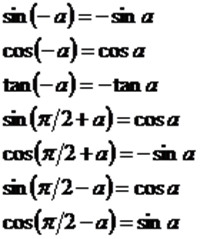一、CORDIC（Coordinate Rotation Digital Computer，坐标旋转数字计算机）算法提供逼近计算的方法，可以将复杂的三角函数、平方根等复杂运算转化为简单的移位相加运算。

二、CORDIC算法有3种旋转系统：圆周系统、线性系统和双曲系统。每种系统下有2种工作模式：旋转模式和向量模式。

三、圆周系统的旋转模式

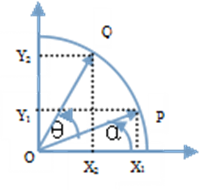
1、在直角坐标系中，将向量OP逆时针旋转θ角得到向量OQ，如图1所示。于是有如下关系式：

  图1 圆坐标系旋转

2、由图1可得以下关系式：

                                                       （式1）

证明：令，则有

                                         （式2）

又因为，代入（式2）可得

                                                        （式3）

故命题得证。

2、通过提取因数，（式3）可转化为

                                                       （式4）

3、去除项（可以简化坐标平面旋转的计算操作），得到伪旋转方程式：

                                                            （式5）

由于，故模值会增大倍。另外，旋转的角度是正确的。

4、我们假设第i次旋转角度为，则第i次伪旋转的表达式为

                                                           （式6） 

对进行一定的限制，使得，即。旋转角度的总和，其中，当时表示向量是逆时针旋转，当时表示向量是顺时针旋转。每次旋转的方向都影响到最终要旋转的累积角度。在的范围内任意角度都可以旋转，满足所有角度的总和为。对于该范围之外的角度，可用三角恒等式变换成该范围内的角度。例如，当目标角度覆盖到时，则需要对目标角度进行预处理。预处理方法一：在原有旋转角度的基础上再添加两级i=0，即将旋转角度总和扩大了，这样目标角度的的取值范围为；预处理方法二：依据正、余弦函数的对称性。

5、在满足第五点的条件下，伪旋转可表示为

                                                          （式7）

其中第三个方程为角度累加器，用来在每次迭代过程中追踪累加的旋转角度；是一个判决算子，用于确定旋转的方向，。

6、令，表征每次旋转时向量模长发生的变化。若总得旋转次数为为n，则总的比例因子K为

                                                            （式8）

当时，K=0.6073。

7、在旋转模式中：。经过n次迭代后得到

                                                 （式9）    

当时，，。通过设置和可以计算和。             

四、圆周系统的向量模式

1、其相应的迭代运算式为：

                                                      （式10）

其中，。

2、经过n(n→∞)次旋转，得到最终结果为

                                                     （式11）

通过设置和来计算。

五、通用的CORDIC方程

                                                    （式12）

• 圆周旋转：

• 线性旋转：

• 双曲线旋转：

六、常用三角函数

（1）两角和公式

（2）倍角公式

（3）诱导公式