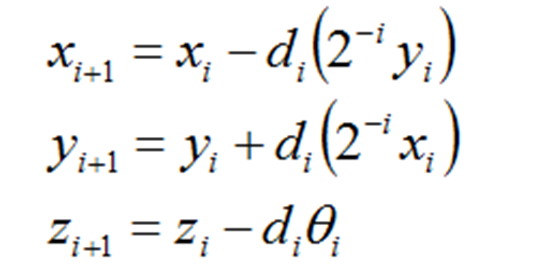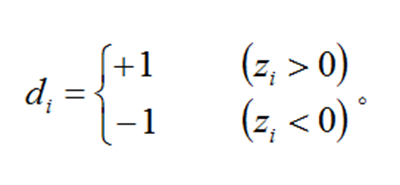【原创】CORDIC算法的FPGA实现
0赞
发表于 2015/3/17 上午2:15:24
阅读(11176)
忙了几天的毕业设计,做了256~16M点FFT窗函数的设计。今晚终于可以写下博客了,嘻嘻。在这次的设计中用到了CORDIC算法,接下来开始举一个简单的例子来说明该算法的FPGA实现。根据上一篇博客的CORDIC算法理论基础,本次设计以圆周系统的旋转模式为依据和迭代法为实现方案。为了方便说明该设计,相位输入位宽为8,迭代次数为8。
(1)由上一篇博客可知,为了让复杂的三角函数转换成简单的移位相加,得对θi进行一定的限制,使tanθi=2-i,即θi=tan-12-i(i=0,1,2...)。这样,我们可以算出每次迭代所对应的旋转角度了。为了快速算出这些旋转角度,我们得寻找一种方便易用、计算能力强大的软件来完成,C、C++等随你选。这里以MATLAB为例:
fid = fopen('rot.txt','w');
for i=0:7
x = atan(2^(-i))/pi*2^7;
rot_angle = atan(2^(-i))*180/pi;
y = dec2bin(x,8);
fprintf(fid,'parameter Rot%d = 8''b',i+1);
fwrite(fid,y);
fprintf(fid,';\t//%8.5fdeg\r\n',rot_angle);
end
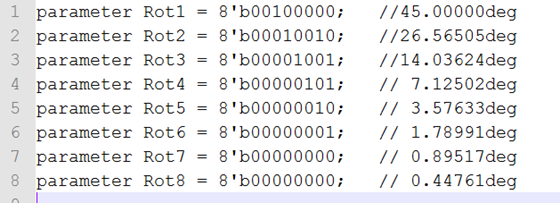
fclose(fid)运行后,产生rot.txt文件,打开后会发现该文件已经包含了本设计中需要的旋转角度:
(2)由于每次旋转都会使向量模长增大1/cosθi倍,n次旋转后模长将增大
1/cosθ0*1/cosθ1*...*1/cosθn-1。为了纠正向量模长,最后得乘以因子
cosθ0*cosθ1*...*cosθn-1。该值的计算也交给MATLAB了。
Init_1 = 1;
fid = fopen('Init.txt','w');
for i = 0:7
cos_data = cos(atan(2^(-i)));
Init_1 = Init_1*cos_data;
end
Init_expand = Init_1*2^7;
Init_data = dec2bin(Init_expand,8);
fprintf(fid,'parameter Init = 8''b');
fwrite(fid,Init_data);
fprintf(fid,'; //%7.5f*2^%d 8次迭代:%7.5f',Init_1,i,Init_1);
fclose(fid)运行后,产生Init.txt文件,内容如下:
(3)有了上面的参数,以及下面的迭代公式和初始值就可以开始设计我们的代码了。
其中di为:
其Verilog HDL设计代码如下:
`timescale 1ns / 1ps
/*******************************************************
Author : CrazyBird
Filename : cordic.v
Data : 2015-3-17
Description : cordic
********************************************************/
module cordic
#(
parameter DATA_WIDTH = 8
)
(
input clk,
input rst_n,
input [DATA_WIDTH-1:0] phase_in,
output reg [DATA_WIDTH-1:0] sin_out,
output reg [DATA_WIDTH-1:0] cos_out
);
//------------------------------------------------
//定义旋转角度
parameter Rot1 = 8'b00100000; //45.00000deg
parameter Rot2 = 8'b00010010; //26.56505deg
parameter Rot3 = 8'b00001001; //14.03624deg
parameter Rot4 = 8'b00000101; // 7.12502deg
parameter Rot5 = 8'b00000010; // 3.57633deg
parameter Rot6 = 8'b00000001; // 1.78991deg
parameter Rot7 = 8'b00000000; // 0.89517deg
//parameter Rot8 = 8'b00000000; // 0.44761deg
parameter Init = 8'b01001101; // 0.60726*2^7 8次迭代:0.60726
//------------------------------------------------
//定义迭代级数
reg [DATA_WIDTH-1:0] x0 ,y0 ,z0 ;
reg [DATA_WIDTH-1:0] x1 ,y1 ,z1 ;
reg [DATA_WIDTH-1:0] x2 ,y2 ,z2 ;
reg [DATA_WIDTH-1:0] x3 ,y3 ,z3 ;
reg [DATA_WIDTH-1:0] x4 ,y4 ,z4 ;
reg [DATA_WIDTH-1:0] x5 ,y5 ,z5 ;
reg [DATA_WIDTH-1:0] x6 ,y6 ,z6 ;
reg [DATA_WIDTH-1:0] x7 ,y7 ,z7 ;
reg [DATA_WIDTH-1:0] x8 ,y8 ,z8 ;
//------------------------------------------------
//限定区间
reg [DATA_WIDTH-1:0] phase_in_reg;
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
phase_in_reg <= 8'h0;
else
begin
case(phase_in[7:6])
2'b00 : phase_in_reg <= phase_in;
2'b01 : phase_in_reg <= phase_in - 8'h40;
2'b10 : phase_in_reg <= phase_in - 8'h80;
2'b11 : phase_in_reg <= phase_in - 8'hc0;
endcase
end
end
//------------------------------------------------
//初始值
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x0 <= 8'h00;
y0 <= 8'h00;
z0 <= 8'h00;
end
else
begin
x0 <= Init;
y0 <= 8'h00;
z0 <= phase_in_reg;
end
end
//------------------------------------------------
//第一级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x1 <= 8'h00;
y1 <= 8'h00;
z1 <= 8'h00;
end
else
begin
if(z0[7]==1'b0)
begin
x1 <= x0 - y0;
y1 <= y0 + x0;
z1 <= z0 - Rot1;
end
else
begin
x1 <= x0 + y0;
y1 <= y0 - x0;
z1 <= z0 + Rot1;
end
end
end
//------------------------------------------------
//第二级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x2 <= 8'h00;
y2 <= 8'h00;
z2 <= 8'h00;
end
else
begin
if(z1[7]==1'b0)
begin
x2 <= x1 - {y1[DATA_WIDTH-1],y1[DATA_WIDTH-1:1]};
y2 <= y1 + {x1[DATA_WIDTH-1],x1[DATA_WIDTH-1:1]};
z2 <= z1 - Rot2;
end
else
begin
x2 <= x1 + {y1[DATA_WIDTH-1],y1[DATA_WIDTH-1:1]};
y2 <= y1 - {x1[DATA_WIDTH-1],x1[DATA_WIDTH-1:1]};
z2 <= z1 + Rot2;
end
end
end
//------------------------------------------------
//第三级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x3 <= 8'h00;
y3 <= 8'h00;
z3 <= 8'h00;
end
else
begin
if(z2[7]==1'b0)
begin
x3 <= x2 - {{2{y2[DATA_WIDTH-1]}},y2[DATA_WIDTH-1:2]};
y3 <= y2 + {{2{x2[DATA_WIDTH-1]}},x2[DATA_WIDTH-1:2]};
z3 <= z2 - Rot3;
end
else
begin
x3 <= x2 + {{2{y2[DATA_WIDTH-1]}},y2[DATA_WIDTH-1:2]};
y3 <= y2 - {{2{x2[DATA_WIDTH-1]}},x2[DATA_WIDTH-1:2]};
z3 <= z2 + Rot3;
end
end
end
//------------------------------------------------
//第四级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x4 <= 8'h00000000;
y4 <= 8'h00000000;
z4 <= 8'h00000000;
end
else
begin
if(z3[7]==1'b0)
begin
x4 <= x3 - {{3{y3[DATA_WIDTH-1]}},y3[DATA_WIDTH-1:3]};
y4 <= y3 + {{3{x3[DATA_WIDTH-1]}},x3[DATA_WIDTH-1:3]};
z4 <= z3 - Rot4;
end
else
begin
x4 <= x3 + {{3{y3[DATA_WIDTH-1]}},y3[DATA_WIDTH-1:3]};
y4 <= y3 - {{3{x3[DATA_WIDTH-1]}},x3[DATA_WIDTH-1:3]};
z4 <= z3 + Rot4;
end
end
end
//------------------------------------------------
//第五级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x5 <= 8'h00;
y5 <= 8'h00;
z5 <= 8'h00;
end
else
begin
if(z4[7]==1'b0)
begin
x5 <= x4 - {{4{y4[DATA_WIDTH-1]}},y4[DATA_WIDTH-1:4]};
y5 <= y4 + {{4{x4[DATA_WIDTH-1]}},x4[DATA_WIDTH-1:4]};
z5 <= z4 - Rot5;
end
else
begin
x5 <= x4 + {{4{y4[DATA_WIDTH-1]}},y4[DATA_WIDTH-1:4]};
y5 <= y4 - {{4{x4[DATA_WIDTH-1]}},x4[DATA_WIDTH-1:4]};
z5 <= z4 + Rot5;
end
end
end
//------------------------------------------------
//第六级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x6 <= 8'h00;
y6 <= 8'h00;
z6 <= 8'h00;
end
else
begin
if(z5[7]==1'b0)
begin
x6 <= x5 - {{5{y5[DATA_WIDTH-1]}},y5[DATA_WIDTH-1:5]};
y6 <= y5 + {{5{x5[DATA_WIDTH-1]}},x5[DATA_WIDTH-1:5]};
z6 <= z5 - Rot6;
end
else
begin
x6 <= x5 + {{5{y5[DATA_WIDTH-1]}},y5[DATA_WIDTH-1:5]};
y6 <= y5 - {{5{x5[DATA_WIDTH-1]}},x5[DATA_WIDTH-1:5]};
z6 <= z5 + Rot6;
end
end
end
//------------------------------------------------
//第七级迭代
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
x7 <= 8'h00;
y7 <= 8'h00;
z7 <= 8'h00;
end
else
begin
if(z6[7]==1'b0)
begin
x7 <= x6 - {{6{y6[DATA_WIDTH-1]}},y6[DATA_WIDTH-1:6]};
y7 <= y6 + {{6{x6[DATA_WIDTH-1]}},x6[DATA_WIDTH-1:6]};
z7 <= z6 - Rot7;
end
else
begin
x7 <= x6 + {{6{y6[DATA_WIDTH-1]}},y6[DATA_WIDTH-1:6]};
y7 <= y6 - {{6{x6[DATA_WIDTH-1]}},x6[DATA_WIDTH-1:6]};
z7 <= z6 + Rot7;
end
end
end
//------------------------------------------------
//第八级迭代
//always @(posedge clk or negedge rst_n)
//begin
// if(!rst_n)
// begin
// x8 <= 8'h00;
// y8 <= 8'h00;
// z8 <= 8'h00;
// end
// else
// begin
// if(z7[7]==1'b0)
// begin
// x8 <= x7 - {{7{y7[DATA_WIDTH-1]}},y7[DATA_WIDTH-1:7]};
// y8 <= y7 + {{7{x7[DATA_WIDTH-1]}},x7[DATA_WIDTH-1:7]};
// z8 <= z7 - Rot8;
// end
// else
// begin
// x8 <= x7 + {{7{y7[DATA_WIDTH-1]}},y7[DATA_WIDTH-1:7]};
// y8 <= y7 - {{7{x7[DATA_WIDTH-1]}},x7[DATA_WIDTH-1:7]};
// z8 <= z7 + Rot8;
// end
// end
//end
//------------------------------------------------
//对界定象限的位进行缓存,为后面的输出正余弦值做区间判断
reg [1:0] phase_in_buf [9:0];
always @(posedge clk or negedge rst_n)
begin
if(!rst_n)
begin
phase_in_buf[0] <= 2'b0;
phase_in_buf[1] <= 2'b0;
phase_in_buf[2] <= 2'b0;
phase_in_buf[3] <= 2'b0;
phase_in_buf[4] <= 2'b0;
phase_in_buf[5] <= 2'b0;
phase_in_buf[6] <= 2'b0;
phase_in_buf[7] <= 2'b0;
phase_in_buf[8] <= 2'b0;
phase_in_buf[9] <= 2'b0;
end
else
begin
phase_in_buf[0] <= phase_in[7:6];
phase_in_buf[1] <= phase_in_buf[0];
phase_in_buf[2] <= phase_in_buf[1];
phase_in_buf[3] <= phase_in_buf[2];
phase_in_buf[4] <= phase_in_buf[3];
phase_in_buf[5] <= phase_in_buf[4];
phase_in_buf[6] <= phase_in_buf[5];
phase_in_buf[7] <= phase_in_buf[6];
phase_in_buf[8] <= phase_in_buf[7];
phase_in_buf[9] <= phase_in_buf[8];
end
end
//------------------------------------------------
//输出正、余弦值
always @ (posedge clk,negedge rst_n)
begin
if(!rst_n)
begin
sin_out <= 8'b0;
cos_out <= 8'b0;
end
else
begin
case(phase_in_buf[8])
2'b00:
begin
sin_out <= y7;
cos_out <= x7;
end
2'b01:
begin
sin_out <= x7;
cos_out <= ~(y7)+1'b1;
end
2'b10:
begin
sin_out <= ~(y7)+1'b1;
cos_out <= ~(x7)+1'b1;
end
2'b11:
begin
sin_out <= ~(x7)+1'b1;
cos_out <= y7;
end
endcase
end
end
endmodule其测试代码:
`timescale 1ns / 1ps /******************************************************* Author : CrazyBird Filename : cordic_tb.v Data : 2015-3-17 Description : test of cordic module ********************************************************/ module cordic_tb; reg clk; reg rst_n; reg [7:0] phase_in; wire [7:0] sin_out; wire [7:0] cos_out; cordic u_cordic ( .clk (clk ), .rst_n (rst_n ), .phase_in (phase_in ), .sin_out (sin_out ), .cos_out (cos_out ) ); parameter PERIOD = 10; initial begin clk = 0; forever #(PERIOD/2) clk = ~clk; end initial begin rst_n = 0; repeat(2)@(negedge clk); rst_n = 1; end always @(posedge clk or negedge rst_n) begin if(!rst_n) phase_in <= 8'b0; else phase_in <= phase_in + 1'b1; end endmodule
(4)测试结果
由仿真结果可以知道功能基本实现,但精度不够高。为了提高精度,可以增加输出相位的位宽和迭代次数。
好,总算讲完了。该睡了,晚安*^_^*