基于累加的PDM算法的由来

- 基于累加的PDM算法(5)

　　作为回顾，这里我想谈一下我的“基于累加的PDM算法”形成的来龙去脉。

　　在“图解Protothreads”一文中，第一个图左上角的“任务1”是我在1983年第一次把PWM用来作为单片机控制的烫头的温度调节。

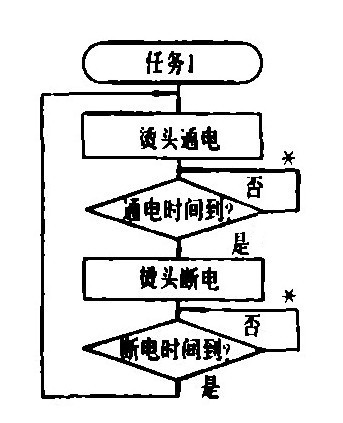
　　事实上，当时我们还没有PWM的概念。我们用“通电时间”和“断电时间”的多少，或者说用“通电时间”占“调节周期”的多少来调节温度。并且还自己取名叫做“时间比例温度调节”。

　　为了避免谐波干扰单片机，我们采用过零触发。以一个正弦波周期（20mS）为一个基本单位，以100个周波（2秒）为调节周期，这样可以达到1%的调节精度。

　　在比例为50%时，通1秒，断1秒。在小烫头上，就可以用灵敏热电偶测到温度的涨落。这就是我对PWM弊端的最早印象。（速热、速冷就要求小的热容量，所以这个“滤波电容”不是想加大就加大的哟。）

　　为什么非要把“通”排在一起，把“断”排在一起呢？分开不就好了吗。这就是我想改变PWM这一方法的缘起。

　　问题是寻找一种算法，怎么重排“通”和“断”，效果最好，而且使单片机以最少资源应对这种控制。

　　幸亏我取了个“比例”的名字，于是就从“保证比例不变”寻找解决办法，这就是算法的核心。

　　每个人自然首先会从自己的经历中寻找解决办法。1973-1974年，我在太原无线电六厂参加了数控铣床计算机的研发，数控铣床及数控线切割直线插补算法给了我启迪。（“青山不老”的新浪博客“说出我的故事28 (2009-11-23 09:09:09)”唤回了我的回忆，也保留了1975年1月数控组为我送行的照片）。

　　数控机床走一条(0,0)-(100,100)的斜线，绝对不会先在X方向走100步，然后在Y方向走100步。而是以一种最合理的方式走出一条微细锯齿形的斜线（无需在此细表）。

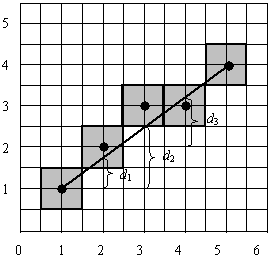
直线插补（借用网上图片）

　　虽然数控走斜线算法与PWM毫不相干，但是“他山之石，可以为错”。为何不可对PWM按时间轴进行插补，而避免PWM那样把所有1都放在一起输出？于是，参照了数控直线插补算法，(1)文中“基于累加的PDM”的算法就应运而生了。当然，最后简化为“一条加法，进位位输出”[(2)文]，那是利用MCU的ALU特性的特例而已。

　　不久前网上看到 ，有同仁说，“只用PDM，抛弃PWM”。我赞同这样的观点。自从1983年那回用“时间比例调节”这种“类PWM方法”作为温度调节之后，找到了“基于累加的PDM算法”。30年来，我没有再使用PWM（即便MCU内带了PWM）。而“基于累加的PDM”在各种产品应用中经受了考验：温控、电脑绣花机主轴调速、电动自行车调速、用单片机数字端口线输出真人语音及带和弦的乐声、LED调光、还把双位电磁阀当作比例阀来使用，等等。

　　当然，话也不是这么绝对，对于低速的应用，MCU内带的PWM还是方便的。但是，要让MCU数字口做仿“D类音频”输出，PWM怕就力不从心了。

　　从PDM的定义讲，PWM和“基于累加的PDM”都是PDM的特例。但是，他们是PDM的两个极端：PWM具最粗糙的的脉冲分布（所有1排在一起，全部0排在一起）；而“基于累加的PDM”具有最均匀的脉冲分布。这就是它们区别的根本所在。

The Origin Of The PDM Algorithm Based On Addition

- A PDM Algorithm Based On Addition (5)

===

FY_ZHU

2013-08-28 BOS-MA

基于累加的PDM算法(1) - 只用一条加法指令实现的PWM算法，软硬都行

基于累加的PDM算法(2) - 基于累加的PDM算法的原理

基于累加的PDM算法(3) - 硬件PWM与基于累加的硬件PDM的比较

基于累加的PDM算法(4) - 如何用PSoC UDB实现硬件PDM