johnllon

高​斯​函​数

0赞
发表于 11/6/2015 9:23:02 PM 阅读（1810）

高斯函数


高斯函数的形式为


的函数。其中 a、b 与 c 为实数常数 ，且a > 0.

c2 = 2 的高斯函数是傅立叶变换的特征函数。这就意味着高斯函数的傅立叶变换不仅仅是另一个高斯函数，而且是进行傅立叶变换的函数的标量倍。

高斯函数属于初等函数，但它没有初等不定积分。但是仍然可以在整个实数轴上计算它的广义积分（参见高斯积分）：



    高斯函数的不定积分是误差函数。在自然科学、社会科学、数学以及工程学等领域都有高斯函数的身影，这方面的例子包括：

    http://zh.m.wikipedia.org/wiki/%E9%AB%98%E6%96%AF%E5%87%BD%E6%95%B8


    高斯分布函数解析


    高斯模糊是一种图像模糊滤波器，它用正态分布计算图像中每个像素的变换。N 维空间正态分布方程为


    在二维空间定义为

    其中 r 是模糊半径 (r2 = u2 + v2)，σ 是正态分布的标准偏差。在二维空间中，这个公式生成的曲面的等高线是从中心开始呈正态分布的同心圆。分布不为零的像素组成的卷积矩阵与原始图像做变换。每个像素的值都是周围相邻像素值的加权平均。原始像素的值有最大的高斯分布值，所以有最大的权重，相邻像素随着距离原始像素越来越远，其权重也越来越小。这样进行模糊处理比其它的均衡模糊滤波器更高地保留了边缘效果，参见尺度空间实现。

    理论上来讲，图像中每点的分布都不为零，这也就是说每个像素的计算都需要包含整幅图像。在实际应用中，在计算高斯函数的离散近似时，在大概3σ距离之外的像素都可以看作不起作用，这些像素的计算也就可以忽略。通常，图像处理程序只需要计算  (6 \sigma + 1) \times (6 \sigma + 1)  的矩阵就可以保证相关像素影响。

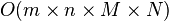    除了圆形对称之外，高斯模糊也可以在二维图像上对两个独立的一维空间分别进行计算，这叫作线性可分。这也就是说，使用二维矩阵变换得到的效果也可以通过在水平方向进行一维高斯矩阵变换加上竖直方向的一维高斯矩阵变换得到。从计算的角度来看，这是一项有用的特性，因为这样只需要 O(n \times M \times N) + O(m \times M \times N) 次计算，而不可分的矩阵则需要 O(m \times n \times M \times N) 次计算，其中 M,N 是需要进行滤波的图像的维数，m、n 是滤波器的维数。

    对一幅图像进行多次连续高斯模糊的效果与一次更大的高斯模糊可以产生同样的效果，大的高斯模糊的半径是所用多个高斯模糊半径平方和的平方根。例如，使用半径分别为 6 和 8 的两次高斯模糊变换得到的效果等同于一次半径为 10 的高斯模糊效果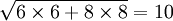，\sqrt{6\times6 + 8\times8} = 10。根据这个关系，使用多个连续较小的高斯模糊处理不会比单个高斯较大处理时间要少。

    在减小图像尺寸的场合经常使用高斯模糊。在进行欠采样的时候，通常在采样之前对图像进行低通滤波处理。这样就可以保证在采样图像中不会出现虚假的高频信息。高斯模糊有很好的特性，如没有明显的边界，这样就不会在滤波图像中形成震荡。

    [cpp] view plaincopy在CODE上查看代码片派生到我的代码片

    1. /*权重函数，使用两个一维高斯函数进行卷积，之所以使用了二维的形式是因为便于统一 调用，下面的调用过程中x或y必有一个为0 */  

    2. float GetGaussianDistribution( float x, float y, float rho ) {  

    3.     float g = 1.0f / sqrt( 2.0f * 3.141592654f * rho * rho );  

    4.     return g * exp( -(x * x + y * y) / (2 * rho * rho) );  

    5. }  

    6.    

    7. void GetGaussianOffsets( bool bHorizontal, D3DXVECTOR2 vViewportTexelSize,  

    8.                          D3DXVECTOR2* vSampleOffsets, float* fSampleWeights ) {  

    9.     // Get the center texel offset and weight  

    10.     fSampleWeights[0] = 1.0f * GetGaussianDistribution( 0, 0, 2.0f );  

    11.     vSampleOffsets[0] = D3DXVECTOR2( 0.0f, 0.0f );  

    12.       

    13.     // Get the offsets and weights for the remaining taps  

    14.     if( bHorizontal ) {  

    15.         for( int i = 1; i < 15; i += 2 ) {  

    16.             vSampleOffsets[i + 0] = D3DXVECTOR2(  i * vViewportTexelSize.x, 0.0f ); //纹理坐标偏移，计算纹理坐标值(像素右方7像素)  

    17.             vSampleOffsets[i + 1] = D3DXVECTOR2( -i * vViewportTexelSize.x, 0.0f );  //像素左方7像素  

    18.   

    19.             fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( float(i + 0), 0.0f, 3.0f ); //原像素左方权重值  

    20.             fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( float(i + 1), 0.0f, 3.0f ); /*我觉得这里应该是float(i+0)因为左边和右边等距点的权重一样*/  

    21.         }  

    22.     }  

    23.   

    24.     else {  

    25.         for( int i = 1; i < 15; i += 2 ) {  

    26.             vSampleOffsets[i + 0] = D3DXVECTOR2( 0.0f,  i * vViewportTexelSize.y );  

    27.             vSampleOffsets[i + 1] = D3DXVECTOR2( 0.0f, -i * vViewportTexelSize.y );  

    28.               

    29.             fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 0), 3.0f );  

    30.             fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 1), 3.0f );  

    31.         }  

    32.     }  

    33. }  

    http://www.cnblogs.com/ttthink/articles/1577789.html



    高斯模糊原理及实现


    高斯模糊即对指定像素和其周围像素进行加权平均来得到最终结果，使用高斯分布作为滤波器。


    高斯分布即为正太分布，1维和2维正态分布密度函数如下




    这里设μ=0， ρ=0.

    u为期望，σ为标准差，μ±σ为函数图像的拐点，σ越大曲线越矮越宽，即采样范围越大。


    在这两个函数中，x，y表示相对于中心像素(0,0)的偏移量(以像素为单位)


    这两个函数的结果表示在x或(x,y)处的像素的权重,或者说在模糊后周围像素分别将产生多少的贡献来影响目标像素.


    一维高斯函数当标准差为1时的一些值:


    G(0) = 0.3989422804
    G(1) = G(-1) = 0.2419707245
    G(2) = G(-2) = 0.0539909665
    G(3) = G(-3) = 0.0044318484


    它们用于计算高斯模糊的含义如下:


    ●在x=0处,即目标像素处,像素颜色的0.39应被保持.

    ●在x=1和x=-1处,像素颜色的0.24应被保持.


    采样像素越多,结果就越精确,根据高斯分布的3σ原则,99.73%的值会落在 (μ-3σ, μ+3σ)中,所以采样像素应根据σ的取值来决定,不宜过多.


    为每个采样像素应用高斯函数计算出它的权重之后,乘上此像素的颜色值,得到此像素为目标像素颜色的贡献值,最后将所有采样点的贡献值加起来就可以得到被模糊后目标像素的颜色.



    使用以上方法进行模糊计算后会出现一个问题,即被模糊后的图像会变暗,当σ较大时尤甚.


    比如:设待模糊的纹理是一张单通道的纯白色纹理,这样每个像素值都为1.

    对某一像素p,在第一遍高斯模糊即横向的模糊后


    p_h_color = G(0)+G(-1)+G(1)+G(-2)+G(2) = 0.990805625.


    要保持原先的亮度,模糊后的结果也应该为1才对,当第二遍模糊处理之后,结果就更糟了


    p_hv_color=0.9818147611.


    所以值需要被修正,使此处模糊后的结果为1

    AugFactor = 1 / p_h_color = 1.009218543


    将这个修正值乘到最后结果p_h_color上和p_hv_color上,即得到正确结果.



    关于1维和2维的高斯函数


    这里有两种选择:

    1.使用1D的版本两次,一次水平,一次垂直(在上一次的基础上), 基于高斯是卷积运算,将2D采样区域分为两个一维向量是可行的.

    2.使用2D的版本一次


    而使用1D版本做两次模糊效率要高于使用2D版本


    假设n为采样区域的大小,即nxn, p为待模糊纹理中的像素数目。

    那么：

    在1D版本中，一共要采样2np次，即对每一个像素需采样横竖各n次。

    在2D版本中，一共要采样n2p次，即对每一像素要采样n2次。

    [cpp] view plaincopy在CODE上查看代码片派生到我的代码片

    1. float GetGaussianDistribution( float x, float y, float rho )   

    2. {  

    3.     float g = 1.0f / sqrt( 2.0f * 3.141592654f * rho * rho );  

    4.     return g * exp( -(x * x + y * y) / (2 * rho * rho) );  

    5. }  

    6. void GetGaussianOffsets( bool bHorizontal, D3DXVECTOR2 vViewportTexelSize,  

    7.                          D3DXVECTOR2* vSampleOffsets, float* fSampleWeights )   

    8. {  

    9.     // Get the center texel offset and weight  

    10.     fSampleWeights[0] = 1.0f * GetGaussianDistribution( 0, 0, 2.0f );  

    11.     vSampleOffsets[0] = D3DXVECTOR2( 0.0f, 0.0f );  

    12.       

    13.     // Get the offsets and weights for the remaining taps  

    14.     if( bHorizontal ) {  

    15.         for( int i = 1; i < 15; i += 2 ) {  

    16.             vSampleOffsets[i + 0] = D3DXVECTOR2(  i * vViewportTexelSize.x, 0.0f );  

    17.             vSampleOffsets[i + 1] = D3DXVECTOR2( -i * vViewportTexelSize.x, 0.0f );  

    18.             fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( float(i + 0), 0.0f, 3.0f );  

    19.             fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( float(i + 1), 0.0f, 3.0f );  

    20.         }  

    21.     }  

    22.     else {  

    23.         for( int i = 1; i < 15; i += 2 ) {  

    24.             vSampleOffsets[i + 0] = D3DXVECTOR2( 0.0f,  i * vViewportTexelSize.y );  

    25.             vSampleOffsets[i + 1] = D3DXVECTOR2( 0.0f, -i * vViewportTexelSize.y );  

    26.               

    27.             fSampleWeights[i + 0] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 0), 3.0f );  

    28.             fSampleWeights[i + 1] = 2.0f * GetGaussianDistribution( 0.0f, float(i + 1), 3.0f );  

    29.         }  

    30.     }  

    31. }  

    代码取自NVIDIA的soft shadows示例中
    http://blog.csdn.net/lovelyloulou/article/details/5485538#

    高斯函数有两个特性

    1：一个高斯函数跟另外一个高斯函数的卷积仍然是一个高斯函数，A*B=C C的标准差的平方是A和B的标准差的平方和，也就是说卷积后的高斯函数更宽，模糊的效果更明显（直观上看，连续做高斯模糊运算，图像会越来越模糊。） 
    2：高斯函数的傅立叶变换仍然是一个高斯函数，如果原来的高斯函数越宽（标准差越大），变换后的高斯函数就越窄（标准差越小），也就是说一个越宽的高斯函数，低通（高阻）滤波的效果越明显，处理后的图像的细节就越不清楚（更模糊）。 

    要对数字图像做高斯模糊，就是用一个符合高斯函数分布的卷积核对数字图像做卷积运算。 
    要确定的有标准差的大小，卷积核的大小，最后的比例系数的大小。 

    一个标准差为1.4的高斯5x5的卷积核： 

    2 4 5 4 2 
    4 9 12 9 4 
    5 12 15 12 5 
    4 9 12 9 4 
    2 4 5 4 2 

    最后乘以比例系数 1/115 

    http://www.360doc.com/content/13/0410/10/10724725_277318941.shtml


Copyright © 2005-2020 《电子技术应用》版权所有 京ICP备10017138号