有一道小学数学题说开去——浅析乒乓操作
1赞前几日,在群里有朋友问有关乒乓操作的问题。大家一起讨论了一番。觉得讨论的结果挺好的,现在总结记录下来和各位网友分享一下。
首先我们来回忆一道经典的小学数学题目(也是姜昆老师的经典相声梗,听过姜昆老师讲的都暴露年龄了):有一个水池,水池完全空的时候只开进水管3小时放满,水池完全满的时候只开排水管6小时排干。那么问题来了。当一开始池子是空的时候,一边灌水一边放水,水池子几个小时被灌满?
分割线,下雨了,得赶紧回家,明天再填——————————————
继续填坑!
很明显,我当然不是到这里来给大家讲小学数学题的。但是这个小学数学题告诉了我们一起浅显的道理:“如果一个池子入水口的入水量大于排水口的出水量,让两个管子一起打开,那么这个池子是一定会被灌满的”。这好像是一句废话,但是废话往往都蕴含着真理。
现在我们换一个视角来看,换成这样的一个场景。现在有两个数据处理模块A和模块B。模块A处理完毕的数据将交给模块B继续处理。模块A的处理速度为100个数据/ms,而模块B的处理速度只有50个数据/ms。那么这个时候B一定是处理不过来的。那现在怎么办呢?在A和B之间加一个水池(Buffer)吧。但即使加了这个Buffer,如果A一直往里面灌水,B也是处理不过来的。那么怎么办呢?
一种办法就是,不让A一直放水,让A间歇性的放水。水开一会,就把入水口A给关掉。让B处理一会,然后把A再打开往里面灌水。这样的缺陷显而易见,A根本发挥不出全力。另外一种办法呢?就是修两个池子,每个池子都接一个排水管B。A先给第一个池子放水,看到池子要满了就换到往第二个池子放水。等第二个池子快满的时候,第一个池子的水已经放的差不多了。A就切换到第一个池子里去继续放水吧。如果A的速度比B高很多,两个池子都装不过来,那么就多搞几个池子。
如果对应到电路设计上面,实质上就是把一个高速的数据流分解为了多个低速的数据流,然后可以让多个低速的处理模块来并行的处理以提高系统整体的处理速度。具体的实现示意图如下:
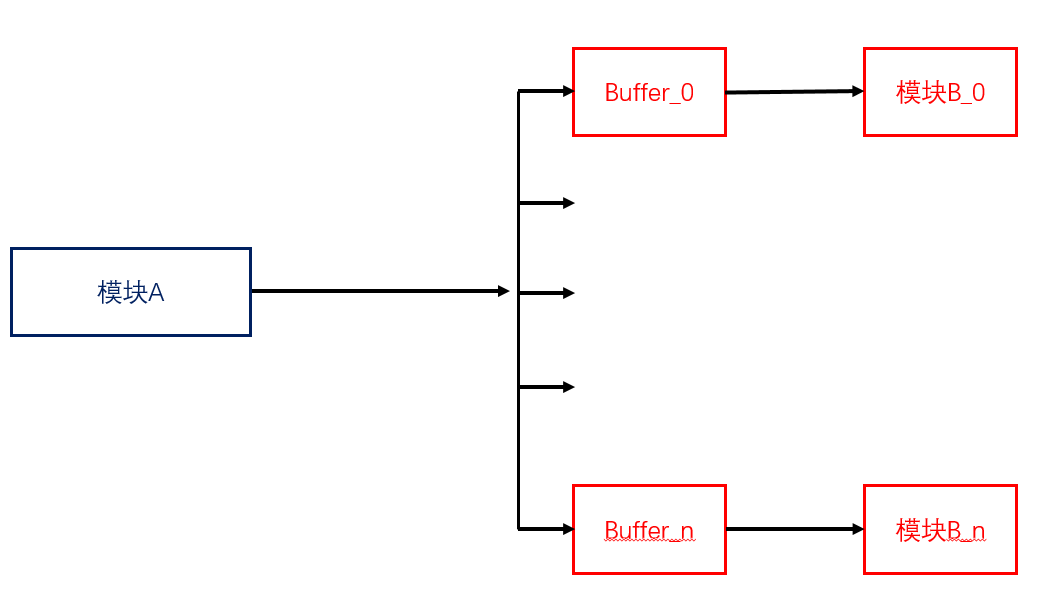
分成多个数据流了,除了模块B本身要复制N次以外,这水池子也要N个。这些都是增加的开销。而这个buffer,也就是水池到底修多大呢?这个就是看设计技巧了。如果设计得当,水池子可以不修那么大也能正常的工作。那如果A和B之间的时钟频率恰好是整数倍关系,那么buffer就设计成一个带使能的寄存器也未尝不可(但是需要在时序约束上考虑多周期路径)。但是为了更稳妥的实现垮时钟域的数据传输,往往需要使用一定容量的异步FIFO来完成。
对于一般的信号处理这类“流计算”系统,数据像水流一样的流进来有流出去。整个处理数据的过程和“排队枪毙”或者“流水线上杀鸡”很类似。用上面的模型解释,也就很直观。但是有很多系统却不能这么简单的来看。比如,如果数据之间存在依赖关系,那么就不能将其简单的展开成多个数据流。这一点在超标量处理器设计中体现的尤为突出。超标量处理器需要对队列中的指令进行一定的重排后,再“发射”出去交给执行单元执行。涉及到超标量处理器的东西太多了,在这里就不详细讲了。
而另外一个用到这类思想的其实是在SoC设计或者说计算机系统设计这个领域。一个高速运转的CPU同时“服务”或者说处理着多个低速IO的数据。因此需要用这样的buffer来把数据暂时存一下。这同样是另外一个大的话题,也不详细讲了。
总之,今天和大家分享的这个呢就是想说:其实很多技术啊,都是有一个朴素的道理在那的。真正把这些技术背后的道理吃透了,也就是是真正“学懂了”。否则,记一堆技术名词,学点软件/硬件操作,没有什么大用。

