以下内容是我个人在反复阅读《FPGA那些事儿--TimeQuest静态时序分析》之后的一点理解，所有的截图都是截自原文。

写这篇文章的目的有如下几点：

1、向akuei2致敬，表明我们大家都很关注他的文章，望再接再厉多出精品，造福我们这些“小白”，嘿嘿。

2、发表一些自己的看法，自我总结，大家一起学习讨论。

3、说出自己曾经的困惑，帮助和我有同样困惑的人。

言归正传：

       接下来主要是对，原文中“FPGA对外模型”部分的理解

就FPGA“内部约束”而言,其实最多就是两句话，一是告诉它时钟，二是PLL的约束。

//时钟约束（50M时钟的情况下）

create_clock -name CLK -period 20.000 [get_ports {CLK}]

//PLL约束

derive_pll_clocks

derive_clock_uncertainty

只要程序没有乱用组合逻辑，一般约束通过是没有问题的。

相反，如果涉及到FPGA与外部高速芯片双向通讯，那么就会涉及到output公式和input公式。

      在此之前，我想谈谈是什么是数据的长度？是什么决定了数据的起点和终点？

TimeQuset的时序检查就是每两个寄存器，在一个时钟内传递数据，看数据是否有效（不考虑多周期约束时）。

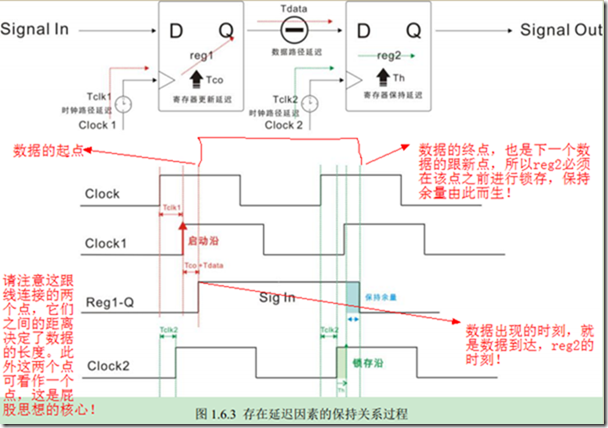
      其实，这幅图真的很经典，（特别是我加上标注之后，哈哈。）可以很好的理检TimeQuset的时序检查。

在启动沿之后，经过一个Tco延时和Tdata延时此时就是数据的启起点，也就是数据到达目的寄存器的时刻。

那数据的终点呢？为什么是在那个地方？（看上图标注）。没错，数据的终点就是“第二个”启动沿经过

一个Tco延时和Tdata延时地方。在此之后迎来的，将是新的数据（下一个数据），所以在该终点之前，目的

寄存器的锁存沿必须将数据锁存住。

      锁存沿，经过Th延时后的时刻，和数据终点时刻之间的那段蓝色部分就是保持余量了。可以试想下如果

Clock2在延时一点，恐怕保持余量就不足了，此时TimeQuest就会检查出这里时序不满足要求。

      由上图可知，一个数据的“出现”和“消失”是和源寄存器的“第一个”启动沿和“第二个”启动沿有关

而数据是否能被完美接收，则要看目的寄存器的锁存沿的位置。

      理解了这一点之后，我们接着看“FPGA对外模型”，说白了就是output公式和input公式。

如果涉及到FPGA与外部高速芯片双向通讯，那么就会涉及到output公式和input公式。

       我们再次回到，“理想建立关系值”和 “理想保持关系值”的问题，作者akuei2用它们简化了对保持余量公式

和建立余量公司的理解。但是在output公式和input公式并没有看到他们的身影，我想这是因为作者发现了更好的

方法——它通过clock skew 这个概念，将FPGA的时钟和芯片的时钟对齐。如下：

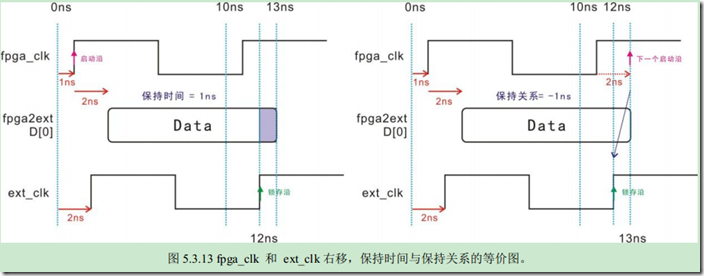
没有平移之前：

平移之后：

 

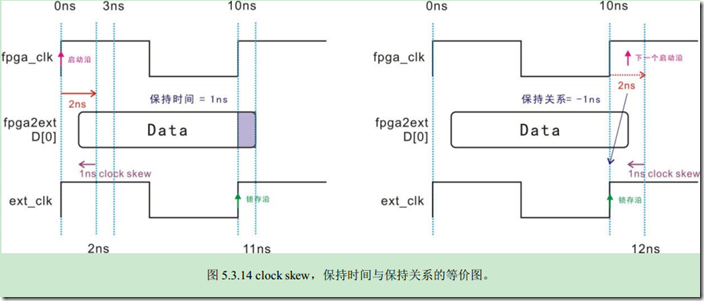
     首先，我们要看清楚，它是怎么平移的，先把数据抛开不管，我们把焦点放在FPGA和IC这两个时钟上面。

这里外部IC是目的寄存器，FPGA是源寄存器，其实就是用源寄存器启动沿前后的延时，去抵消了目的寄存器

启动沿之前的延时（或者说是上一个锁存沿之前的延时）：（1 + 2） – 2 = 1ns；我们同

平移，两个“寄存器”的时钟站在了起跑线上。启动沿经过了1ns数据便出现了，在下一个启动沿延时1

个ns之后该数据结束。时钟对齐之后，建立余量和保持余量就更加的直观的，这真是个好方法啊！！

    写到这里我还发现：源寄存器的“启动沿”和目的寄存器的“锁存沿”之间是建立余量的范围。

源寄存器的“启动沿”和目的寄存器“上一个锁存沿”之间是保持余量的范围。

     铺垫这么多，似乎还没看到output公式和input公式的影子，不急慢慢来。我们知道在约束输入输出引

脚的时候一般会填写一个最大延时值，和最小延时值。这个填完了，引脚约束也就结束了。重要的是这个

最大值和最小值是怎么来的。当然是公式算出来的，呵呵。但是为什么是一个范围呢？

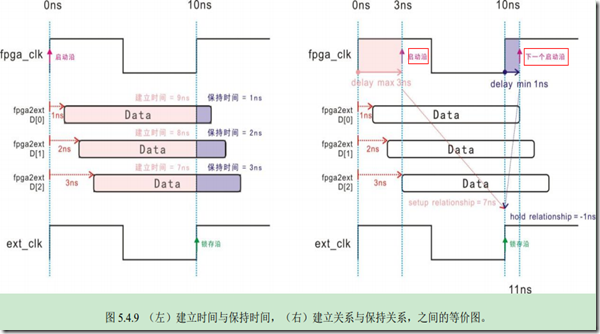
拿USB芯片举个例子，它的的数据总线是16位，分别连接到FPGA的16个引脚，由于每条线路的长短不一，

那么必然导致延时的不均匀，如下图：

从上图，我们可以清楚的看到，如果源寄存器的启动沿之后的延时越久，那么

保持余量就越多，相反建立余量就越少。反过来说如果源寄存器的启动沿之后

的延时越少，那么 保持余量就越少，相反建立余量就越多。总之不管多少都

存在危险，所以只要把两种最极端的情况加以分析就可以了，极端情况满足了

其他的情况必然满足，于是乎我们只要把最极端的值告诉TimeQuest就行了，

也就是说所谓的最大延时值和最小延时值是由于数据的位宽不止一位，外加

线路长短不一造成的。当然，如果数据线只有一位，那么最大延时值和最小

延时值就会相等。（看上图可以更好的理解这点）

接下来就是公式的推理过程了，话说作者通过这种画图的方式真的很棒：

//-----------------加上“寄存器特性”的output公式-----------------

     假设，FPGA作为发送方，也就是源寄存器，IC作为接收方，也就是目的寄存器，

那么就是output公式，那么我们要知道，IC的寄存器锁存时技术参数，及Tsu和Th，

（而不用管作为发送方FPGA的Tco，因为TimeQuest了解FPGA的一切）

先来看Tsu：

观察上图发现，作者将Tsu这段属于IC时间搬移到了FPGA的时钟延时里，这个是

为什么呢？

这里我有必要在做一个说明：

      Tco是属于源寄存器的延时参数，Tsu和Th是属于目的寄存器的延时因素。

      所谓Tsu就是目的寄存器锁存数据所需要的最小准备时间，也就是说在锁存沿

之前的这段时间内，数据必须跟我准备好。Tsu主要影响的是建立时间，它会使建

立时间减少（从上图看的很明显）。还有一个东东也顺便讲讲，Th它是锁存沿之后

所需要的最小锁存时间，也就是说，锁存沿之后这段时间数据必也须存在，不能

没了。Th主要会导致保持时间的减少。

    有的读者发现，怎么一会Tsu把锁存沿左移，一会Th又把锁存沿右移，

锁存沿到底在哪？其实不是这样的，作者表达的意思就是在锁存沿左右这两段时间

内数据必须是稳定存在的，但是为了图像上好理解，就好像锁存沿平移了一样。

好了，说明到此结束～～～～

    回到，之前的问题，为什么将Tsu这段属于IC时间搬移到了FPGA的时钟延时里，

原因很简单，应为TimeQuest只能约束FPGA，不能约束外围的芯片，所以把属于

IC的延时压力算到了FPGA的身上，这种转移是否等价呢？从上图观察到，这种转移

明显是等价的，都是将建立时间减少了0.5ns（即Tsu的时间）。

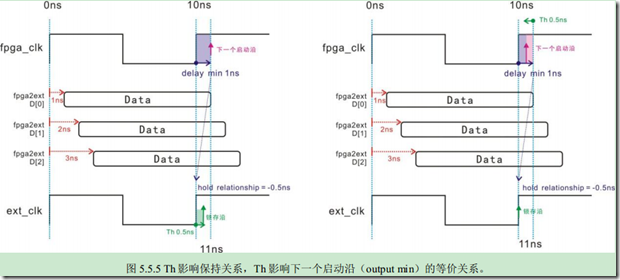
看完Tsu再看Th：

Tsu会导致保持时间的减少，同样我们要把这份属于IC的延时压力转移到作为

发送发（源寄存器）的身上，那么我们就要下一个启动沿之后的延时去抵消它。

   到此，作为接收方的IC的延时压力，都“转移到”FPGA的身上，那么output

公式已经呼之欲出了。

     到这里，可能还会有点疑问，为什么Tsu会算到output max里，而Th会算到output

min里，联系上文，其实就应该有答案了。

     我们知道如果<fpga2ext delay max> - < clock skew >这个部分越大的话，意味着

建立时间越少，而保持时间越多。危险的是建立时间，而Tsu同样是会减少建立时间的，

它会增加建立时间不足的危险性，而我们就是要把最极端，最危险的情况告诉TimeQuest

所以IC的Tsu会加到output max。

    同理，<fpga2ext delay max> - < clock skew >这个部分越小的话，保持时间就会越

少（建立时间越多），Th会让保持时间更少，从而这种情况是最极端的，所以在output min

要减去IC的Th。

output公式总结：

1、output公式中FPGA作为发送方，及源寄存器，外部IC作为接收方，及目的寄存器。

 

2、TimeQuest了解FPGA的一切，而不了解外部芯片，所以当FPGA作为发送方时，FPGA的

Tco是不用管的，TimeQuest自己会考虑进去。TimeQuest想知道的是外部IC的Tsu和Th。

 

3、TimeQuest所能做的就是把属于外部IC的延时压力“转移”到FPGA的身上。

 

4、“时钟到达IC的时间“- “时钟到达FPGA的时间”，即到达目的寄存器的延时减去到达源寄存器的延时

而fpga2ext delay就是Tco加上Tdata，而FPGA的Tco是不用管的，所以只剩下Tdata了。Tdata就是

FPGA引脚到IC引脚的连线的这段距离所要消耗的时间，而数据的位宽不止一位的话，这个线自然有长

有短所以就出现了fpga2ext delay max 和 fpga2ext delay min.

 

5 、Tsu算到fpga2ext delay max 里，Th算到fpga2ext delay min里。将最极端的情况告诉TimeQuest

它才会告诉你最真实的保持余量和建立余量～～～

未完待续～～