1.传感器排布与赛道信息解算的数学模型

　　假设载流导线无限长直，电流为()it 。不妨假设电感为理想电感，即空间尺寸可忽略不计，电感铁芯工作在线性区[1]。

　　空间一点某一方向上的磁感应强度为()Bt，由毕奥--萨伐尔定律[2]得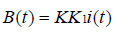其中K由空间位置决定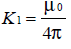，不妨将K称为空间函数，电感不同的放置方式，对应不同的K。若迹线为无限长直的导线，则相同的电感放置方式下，K的表达式不变。

　　设()et为电感的开路感应电动势，由法拉第电磁感应定律[3]得：

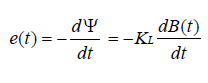　　，其中LK由电感的参数决定，是常数。

　　将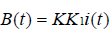进行拉氏变换得其中

　　将进行拉氏变换得其中

　　将电感到A/D转换之间的电路设计为线性时不变系统，设其传递函数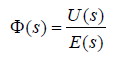则

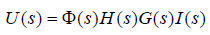
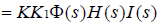在小车起跑前测得

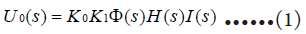
　　在小车起跑后测得

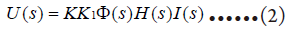
　　式(2)除以(1)得

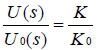
　　发现电路的传递函数和电流等与空间函数无关的项都被消去了。对于不同的电感排布方式，只要先得出空间函数K，然后运用该方法就能得出其对应的迹线信息解算表达式。这也正是本文要做的工作。为方便起见，将该方法称为“法一”。