前面的一篇文章中介绍了两种插值方法，最近邻插值和（双）线性插值：

http://blog.chinaaet.com/justlxy/p/5100052604

我们知道，最近邻插值运算简单，消耗的资源很少（时间资源或者逻辑资源），但是会引入严重的失真（表现为马赛克），双线性插值效果较好，能够很好地恢复图像的信息，但是其中包含较多的小数运算（主要是乘法），即使我们采用定点小数来代替浮点小数，仍然会有较大的开销（时间上和空间上的）。

今天介绍一种适合FPGA上实现的图像插值算法——9点插值法，只需要进行加法运算和移位运算即可，其插值效果要比最近邻插值法好很多，但是比双线性插值法要差一点。具体的原理如下：

上图中，黑色的点表示实际的点（x和y均为整数值），灰色的点表示虚拟的点，其像素值可以由实际的点的像素值获得：

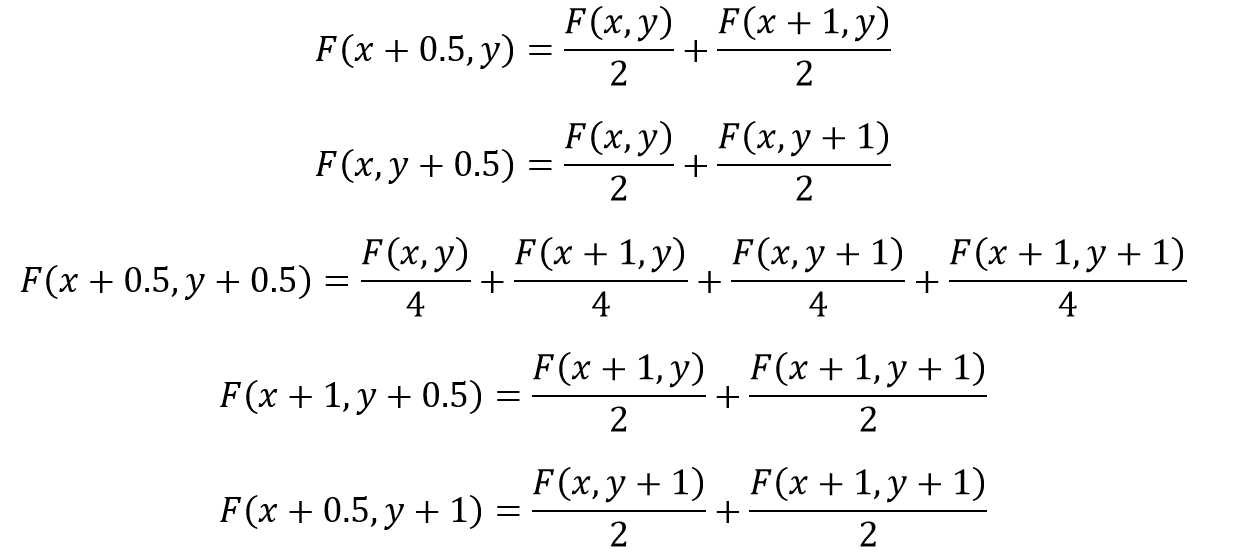
现将上图分为四个区域，Area1到Area4，当校正之后的点Q1落在Area 1时，其像素值为：

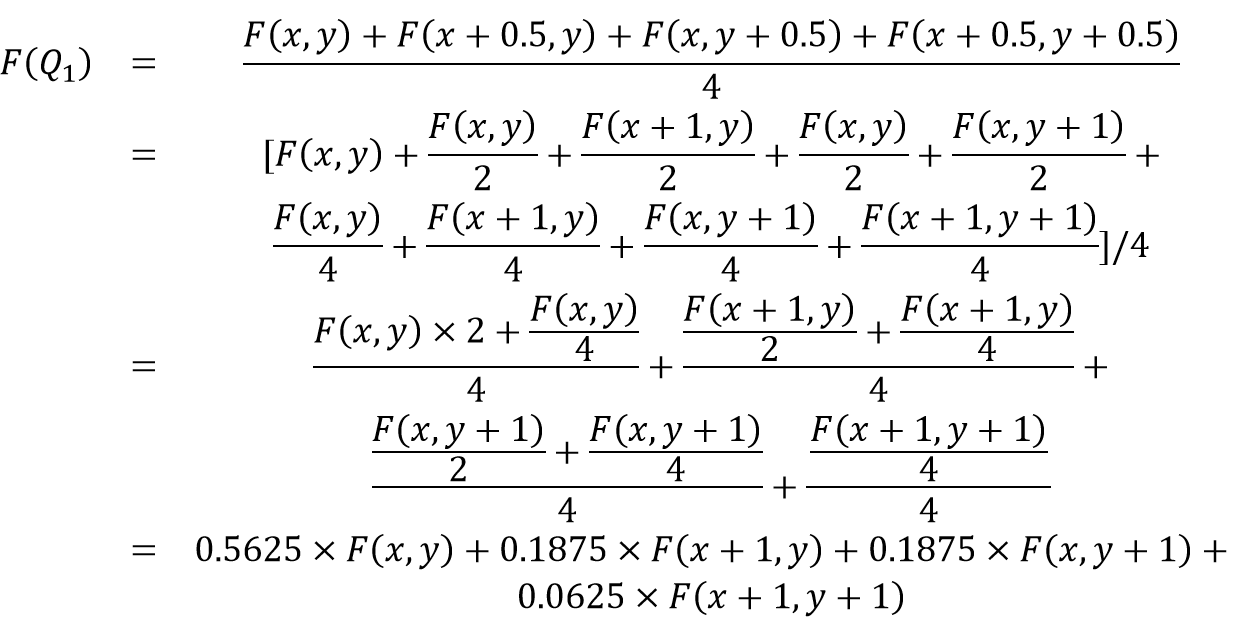
同理可得，Q2,Q3,Q4的像素值为：

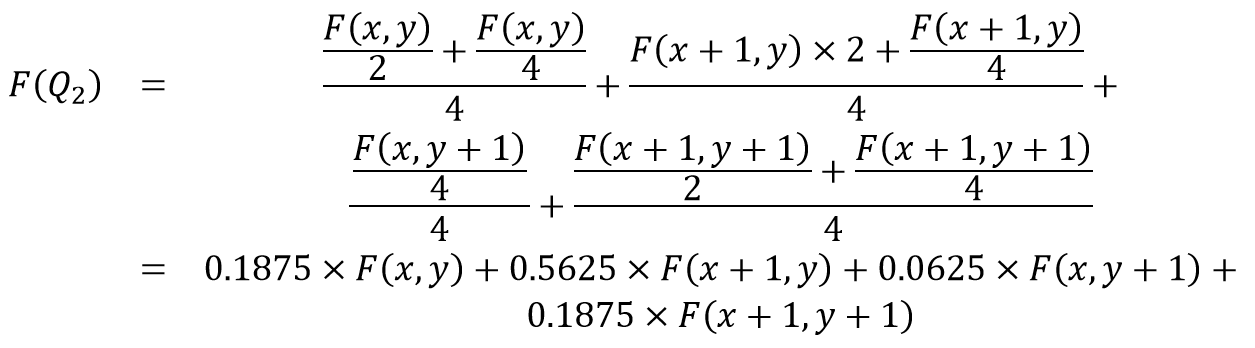
当然，为了进一步降低计算量，我们可以做一个简单的优化，将0.1875用1/4替代，将0.5625用1/2替代，而0.0625即为1/16。此时消耗的资源（时间上和空间上的）又显著地降低了！

此外，还有一种更加简化的9点插值法，其思想就是选取与校正之后的点Q最为接近的某个点（9个点之一）的像素值作为Q的像素值，当Q的坐标为定点小数的表示方式时，这种判断方式还是很方便的，其效果要比上面介绍的稍微差一点，但是却进一步降低了计算量。

举例说明：当Q的坐标为定点小数时，Q的坐标的整数部分决定了四个实际的点的坐标，如果Q的x坐标的小数部分第一位为1，且y坐标的小数部分第一位也为1，则认为Q落在Area 4中。此时，进一步判断，如果Q的x坐标的小数部分的第二位为1，且y坐标的小数部分的第二位也为1，则认为离Q最近的点是（x+1，y+1）……其他的情况依次类推。