前几天写了一篇关于CORDIC算法的文章，可能关于K值并没有说的特别清楚，今天刚好遇到有人问我这个问题。正好借此机会来详细说明一下。

首先，之前的文章是：

http://blog.chinaaet.com/justlxy/p/5100052271

之前的文章已经提到了，每次迭代中的Ki为

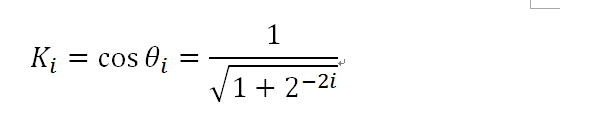
很显然，Ki的值是小于1的。在实际的运算过程中，为了避免浮点除法运算和平方根运算，都是直接忽略掉Ki的。这就导致了一个问题，运算之后的向量的模长变大了，与实际的长度刚好为K倍的关系，其中，K为：

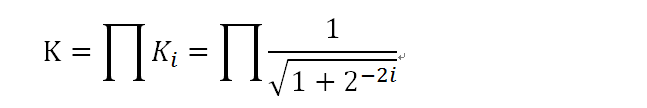
也就是说，如果想要消除计算模长的变化，只需要除以K值既可以了。熟悉数列的童鞋，应该可以轻松的计算出来K值的大小，当n取无穷大时（即迭代无穷次时），K=0.607252935……，而1/K = 1.646760258，即前面的文章中所提到的Altera的IP中出现的常量。当然，实际情况下，n不可能是无穷大，所以实际的K值也会有些差别。但是一般情况下，当迭代次数大于16次时，1/K的值就已经很接近1.6467605……了，所以Altera直接将K作为常量处理也没什么不妥的。

但是，当迭代次数较小时，此时K值的取值带来的误差就比较大了；与此同时，需要注意的是，迭代次数较小时，CORDIC的算法本身的误差就已经很大了……此时再去争论K值带来的误差，实际上是毫无意义的！

关于K的具体取值，在Lattice和Xilinx的文档中并为明确提及，不过，个人觉得，应该也是采取了和Altera相似的处理方法。对于那些想自己编程实现CORDIC功能的朋友们，可以分别计算各个n值（迭代次数）下的K的真实值，并将其存放在ROM中，以供算法调用。显然，这是一种面积换取精度的做法……

对于想深入了解CORDIC算法原理，及其发展史的朋友，推荐几篇论文给大家，英文hold不住的童鞋就算了……

1、CORDIC被首次提出的论文：The CORDIC Computing Technique.pdf

2、CORDIC算法的50年发展综述：50 Years of CORDIC Algorithms Architectures and Applications.pdf

如有不足，欢迎补充！