FPGA定点小数计算(Verilog版)第六篇——平方根运算
3赞
发表于 11/24/2017 4:52:46 PM
阅读(9091)
好久之前挖的坑,今天终于给填上了,本文所介绍的平方根运算的VHDL源码来自OpenCore,有兴趣的可以自行下载阅读。本想直接找一个Verilog版本的,来参考参考的,结果找了好久都没有找到……于是乎,花了两天时间补习了一波VHDL,勉强能够看懂写的是嘛意思了……至于VHDL,实在是无力吐槽了,太变态了,还是Verilog好,哈哈哈……
VHDL源码如下:
library ieee; use ieee.std_logic_1164.all; use ieee.numeric_std.all; entity square_root is generic( WIDTH: positive := 32 ); port( clk: in std_logic; res: in std_logic; ARG: in unsigned (WIDTH - 1 downto 0); Z: out unsigned (WIDTH - 1 downto 0) ); end entity square_root; architecture rtl of square_root is constant SQRT_LUT_K: positive := 8; constant SQRT_LUT_N: positive := 128; --2^(K-1) constant SQRT_ITER: positive := 3; type sqrt_table is array (natural range <>) of unsigned (WIDTH-1 downto 0); type pipe is array (natural range <>) of unsigned (WIDTH - 1 downto 0); constant SQRT_TABLE_1 : sqrt_table(0 to SQRT_LUT_N - 1) := ( x"B504F334", x"B44F9363", x"B39C5088", x"B2EB2034", x"B23BF845", x"B18ECED9", x"B0E39A54", x"B03A5158", x"AF92EAC8", x"AEED5DC0", x"AE49A198", x"ADA7ADE2", x"AD077A62", x"AC68FF15", x"ABCC3428", x"AB3111FD", x"AA979122", x"A9FFAA55", x"A9695681", x"A8D48EBE", x"A8414C4B", x"A7AF8892", x"A71F3D24", x"A69063BA", x"A602F631", x"A576EE88", x"A4EC46E7", x"A462F992", x"A3DB00F1", x"A354578E", x"A2CEF80E", x"A24ADD38", x"A1C801EF", x"A1466132", x"A0C5F61D", x"A046BBE7", x"9FC8ADE0", x"9F4BC775", x"9ED00428", x"9E555F96", x"9DDBD571", x"9D636184", x"9CEBFFB1", x"9C75ABED", x"9C006245", x"9B8C1ED8", x"9B18DDDC", x"9AA69B99", x"9A355468", x"99C504B9", x"9955A90B", x"98E73DF0", x"9879C009", x"980D2C0B", x"97A17EB9", x"9736B4E7", x"96CCCB78", x"9663BF5F", x"95FB8D9D", x"95943342", x"952DAD6B", x"94C7F945", x"94631407", x"93FEFAF9", x"939BAB6C", x"933922C1", x"92D75E64", x"92765BCB", x"9216187A", x"91B69200", x"9157C5F6", x"90F9B200", x"909C53CF", x"903FA91C", x"8FE3AFAB", x"8F886548", x"8F2DC7CC", x"8ED3D518", x"8E7A8B16", x"8E21E7B8", x"8DC9E8FC", x"8D728CE5", x"8D1BD182", x"8CC5B4E8", x"8C703534", x"8C1B508D", x"8BC70521", x"8B735123", x"8B2032D2", x"8ACDA871", x"8A7BB04A", x"8A2A48B2", x"89D97000", x"89892494", x"893964D5", x"88EA2F2F", x"889B8216", x"884D5C04", x"87FFBB77", x"87B29EF6", x"8766050B", x"8719EC47", x"86CE5342", x"86833897", x"86389AE8", x"85EE78DC", x"85A4D11E", x"855BA261", x"8512EB59", x"84CAAAC3", x"8482DF5D", x"843B87ED", x"83F4A33B", x"83AE3016", x"83682D4F", x"832299BD", x"82DD743A", x"8298BBA6", x"82546EE5", x"82108CDC", x"81CD1478", x"818A04A6", x"81475C5C", x"81051A8E", x"80C33E38", x"8081C657", x"8040B1ED", x"80000000" ); constant SQRT_TABLE_2 : sqrt_table(0 to SQRT_LUT_N -1) := ( x"FFFFFFFF", x"FE000000", x"FC07F020", x"FA17A17A", x"F82EE698", x"F64D9365", x"F4737D1D", x"F2A07A45", x"F0D4629B", x"EF0F0F0F", x"ED5059B2", x"EB981DAE", x"E9E63740", x"E83A83A8", x"E694E122", x"E4F52EE0", x"E35B4CFB", x"E1C71C72", x"E0387F1E", x"DEAF57AC", x"DD2B8994", x"DBACF915", x"DA338B2B", x"D8BF258C", x"D74FAE9F", x"D5E50D79", x"D47F29D4", x"D31DEC0D", x"D1C13D1C", x"D0690690", x"CF15328C", x"CDC5ABBF", x"CC7A5D62", x"CB333333", x"C9F01971", x"C8B0FCD7", x"C775CA9A", x"C63E7064", x"C50ADC51", x"C3DAFCEA", x"C2AEC126", x"C1861862", x"C060F25E", x"BF3F3F3F", x"BE20EF88", x"BD05F418", x"BBEE3E26", x"BAD9BF44", x"B9C86953", x"B8BA2E8C", x"B7AF0172", x"B6A6D4DB", x"B5A19BE3", x"B49F49F5", x"B39FD2BE", x"B2A32A33", x"B1A9448C", x"B0B21643", x"AFBD9411", x"AECBB2ED", x"ADDC680B", x"ACEFA8DA", x"AC056B01", x"AB1DA461", x"AA384B0F", x"A9555555", x"A874B9B3", x"A7966ED8", x"A6BA6BA7", x"A5E0A72F", x"A50918B1", x"A433B799", x"A3607B7F", x"A28F5C29", x"A1C05183", x"A0F353A5", x"A0285ACC", x"9F5F5F5F", x"9E9859EA", x"9DD3431B", x"9D1013CA", x"9C4EC4EC", x"9B8F4F9E", x"9AD1AD1B", x"9A15D6C0", x"995BC60A", x"98A37495", x"97ECDC1D", x"9737F679", x"9684BDA1", x"95D32BA6", x"95233AB7", x"9474E51D", x"93C8253D", x"931CF593", x"927350B9", x"91CB315D", x"91249249", x"907F6E5D", x"8FDBC091", x"8F3983F2", x"8E98B3A6", x"8DF94AE6", x"8D5B4502", x"8CBE9D5E", x"8C234F73", x"8B8956CC", x"8AF0AF0B", x"8A5953E1", x"89C34116", x"892E727F", x"889AE409", x"880891AC", x"87777777", x"86E79187", x"8658DC08", x"85CB533A", x"853EF369", x"84B3B8F2", x"8429A043", x"83A0A5D4", x"8318C632", x"8291FDF2", x"820C49BA", x"8187A63F", x"81041041", x"8081848E", x"80000000" ); constant one_and_half: unsigned(WIDTH-1 downto 0) := x"C0000000";--"11000000000000000000000000000000"; signal n: pipe(0 to SQRT_ITER); signal n_next: pipe(0 to SQRT_ITER); signal d: pipe(0 to SQRT_ITER); signal d_next: pipe(0 to SQRT_ITER); signal r: pipe(0 to SQRT_ITER); signal r_next: pipe(0 to SQRT_ITER); signal rsqr: pipe(0 to SQRT_ITER); signal rsqr_next: pipe(0 to SQRT_ITER); begin -- pipe stages process(clk) is begin if rising_edge(clk) then for i in 0 to SQRT_ITER loop if (res = '0') then n(i) <= (others => '0'); d(i) <= (others => '0'); r(i) <= (others => '0'); rsqr(i) <= (others => '0'); else n(i) <= n_next(i); d(i) <= d_next(i); r(i) <= r_next(i); rsqr(i) <= rsqr_next(i); end if; end loop; end if; end process; -- process inputs for the next stage process(d,r,rsqr,n,ARG) is variable n_extended : unsigned(2*WIDTH-1 downto 0); variable d_extended : unsigned(2*WIDTH-1 downto 0); variable r_next_tmp : unsigned(WIDTH-1 downto 0); variable d_shift : unsigned(WIDTH-1 downto 0); variable rsqr_extended : unsigned(2*WIDTH-1 downto 0); variable index_vec : unsigned(SQRT_LUT_K-2 downto 0); variable index : integer; begin n_next(0) <= ARG; d_next(0) <= ARG; index_vec := ARG(WIDTH - 3 downto WIDTH - SQRT_LUT_K - 1); index := to_integer(index_vec); r_next(0) <= SQRT_TABLE_1(index); rsqr_next(0)<= SQRT_TABLE_2(index); for i in 1 to SQRT_ITER loop --operations n_extended := n(i-1) * r(i-1); d_extended := d(i-1) * rsqr(i-1); d_shift := "0" & d_extended(2*WIDTH -2 downto WIDTH); r_next_tmp := one_and_half - d_shift; rsqr_extended := r_next_tmp * r_next_tmp; --assignments n_next(i) <= n_extended(2*WIDTH-2 downto WIDTH-1); d_next(i) <= d_extended(2*WIDTH-2 downto WIDTH-1); rsqr_next(i) <= rsqr_extended(2*WIDTH-2 downto WIDTH-1); r_next(i) <= r_next_tmp; end loop; end process; -- assign output Z <= n(SQRT_ITER); end rtl;
因为原本的程序(VHDL)中存在迭代运算和长组合逻辑(主要是乘法运算),虽然用的资源不多,但是速度实在不能忍,只有30M左右……于是乎,我便把所有的设计都Pipeline一遍,同时把乘法器和ROM替换为Clarity生成的Module。目前实现效果如下(如果需要,还可以再优化优化):
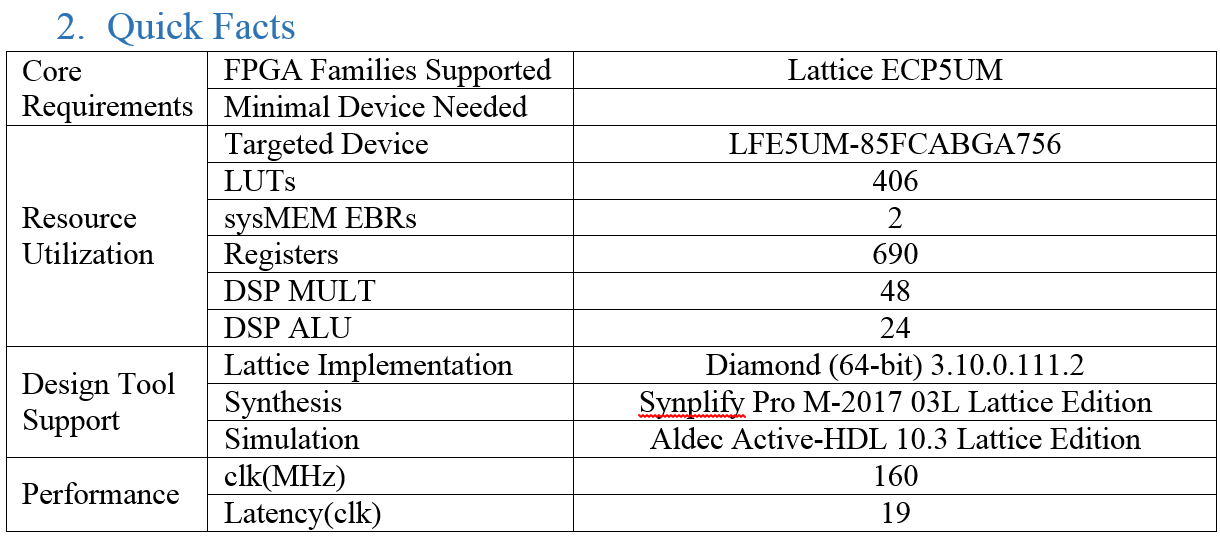
具体可以参考该文档,文档中还详细描述了源码中定点小数的数据格式:
使用Synplify Pro综合得到的RTL视图(顶层)如下:

目前完成了功能仿真测试,初步的时序约束和静态时序分析,功能仿真的效果如下图:

Verilog的源码,以及仿真脚本和ROM初始化文件之类的太长了,就补贴出来了。

