FPGA定点小数计算(四)——平方根倒数
2赞0 引言
在图像处理及3D图形编程时,经常要求解特征向量的长度或者将向量归一化,其中尤为关键的运算便是平方根倒数运算。而开平方根运算与倒数运算都是很复杂的过程,如果将平方根倒数运算分为这两个步骤则需要更多的时间开销和空间开销。而采用常规的浮点运算单元(FPU)来求解的话,同样需要很长的计算时间。
本文介绍一种基于牛顿迭代法(又称Newton-Raphson算法)的平方根倒数算法的HDL实现,只需要进行一次到两次迭代便可获得相对精确的结果。在一些实时图像处理场合中,对算法的运算速度和Latency要求较高,因此可以采用定点小数适当地降低精度以获得更高的性能。
1 牛顿迭代法求平方根倒数原理
算法原理
牛顿迭代法的基本思想是将非线性方程线性化,以线性方程的解逼近非线性方程的解。为了计算x的平方根倒数![]() ,可以先构造函数
,可以先构造函数

该函数的正根即为要求的解。牛顿迭代法的精髓在于,可以先猜测一个值![]() ,然后基于这个值,采用以下的迭代式,以获得更加精确的值:
,然后基于这个值,采用以下的迭代式,以获得更加精确的值:

为了方便计算,上式可以简化为:

该算法的C语言实现如下:
float InvSqrt(float x) {
float xhalf = 0.5f * x;
// Using input x as the first guess y0
x = x * (1.5f - xhalf * x * x); // Newton step, repeating increases accuracy
x = x * (1.5f - xhalf * x * x); // Newton step
x = x * (1.5f - xhalf * x * x); // Newton step
x = x * (1.5f - xhalf * x * x); // Newton step
return x;
} |
The Magic Number
牛顿迭代法有两个重要影响因素:猜测值(又称为初始值)和迭代次数。一个合适的猜测值可以减少迭代次数,甚至只进行一到两次迭代操作,却可以实现相同的运算精度。然而这样的猜测值却是很难寻找的,所以为了保证运算的精度,一般需要4~5次的迭代操作,这样的开销还是很大的。
数学的美妙之处在于,看似变幻莫测,却存在着一些恒定不变的常量。有人发现了一种神奇的猜测值寻找方法,无论输入的值是多少,采用其获得的猜测值,都可以只通过1~2次迭代便获得较为精确的结果。
在介绍这种方法之前,不得不先说一个经典游戏——雷神之锤3。雷神之锤3(Quake-III Arena)是90年代的经典游戏之一。该系列的游戏不但画面和内容不错,而且即使计算机配置低,也能极其流畅地运行。这要归功于它3D引擎的开发者约翰-卡马克(John Carmack)。事实上早在90年代初DOS时代,只要能在PC上搞个小动画都能让人惊叹一番的时候,John Carmack就推出了石破天惊的Castle Wolfstein, 然后再接再励,doom, doomII, Quake...每次都把3D技术推到极致。他的3D引擎代码极度高效,几乎是在压榨PC机的每条运算指令。当初MS的Direct3D也得听取他的意见,修改了不少API。
前一段时间,Quake的开发商ID SOFTWARE 遵守GPL协议,公开了Quake-III的原代码,让世人有幸目睹Carmack传奇的3D引擎的原码。大家在其底层的数学运算函数库中,发现了这样一段代码。它的作用是将一个数开平方并取倒数,经测试这段代码比(float)(1.0/sqrt(x))快4倍:
float InvSqrt(float x) {
float xhalf = 0.5f * x;
int i = *(int*)&x; // Get bits for floating value
i = 0x5f3759df - (i >> 1); // Gives initial guess y0
x = *(float*)&i; // Convert bits back to float
x = x * (1.5f - xhalf * x * x); // Newton step, repeating increases accuracy
return x;
} |
John Carmack牛掰的地方在于,他采用了一个神奇的常数0x5f3759df来计算初始猜测值。普渡大学的数学家Chris Lomont看了以后觉得有趣,决定要研究一下Carmack弄出来的这个猜测值有什么奥秘。Lomont也是个牛人,在精心研究之后从理论上也推导出一个最佳猜测值,和Carmack的数字非常接近, 0x5f37642f。传奇并没有在这里结束。Lomont计算出结果以后非常满意,于是拿自己计算出的起始值和Carmack的神秘数字做比赛,看看谁的数字能够更快更精确的求得平方根。结果是Carmack赢了……谁也不知道Carmack是怎么找到这个数字的。最后Lomont怒了,采用暴力方法一个数字一个数字试过来,终于找到一个比Carmack数字要好上那么一丁点的数字,虽然实际上这两个数字所产生的结果非常近似,这个暴力得出的数字是0x5f375a86。
2 Verilog HDL算法实现
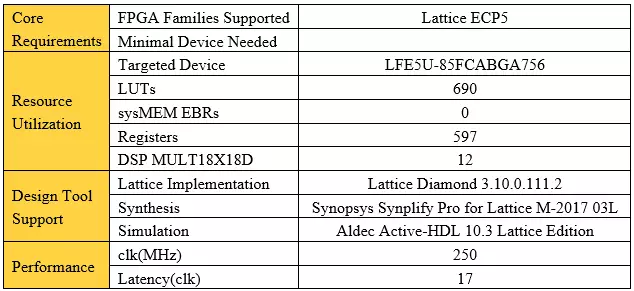
为了提高算法的运算速度,并减小Latency,算法采用定点小数进行运算。然而,John Carmack提出的猜测值计算方法却是基于浮点数的。因此需要先将输入值转换成浮点数,获得猜测值后,在将其转换为定点数。程序中定点数的格式为:

即,
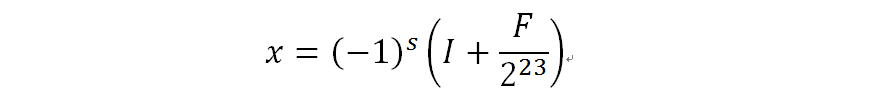
RTL视图如下:

其中,牛顿迭代的RTL视图如下:
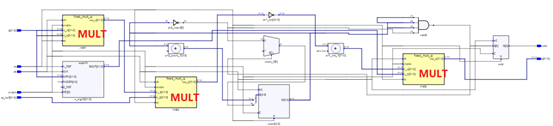
详细信息如下:
如果对Latency要求较高的话,还可以将迭代公式转化为:
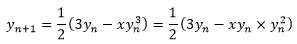
此时,牛顿迭代的RTL视图如下:
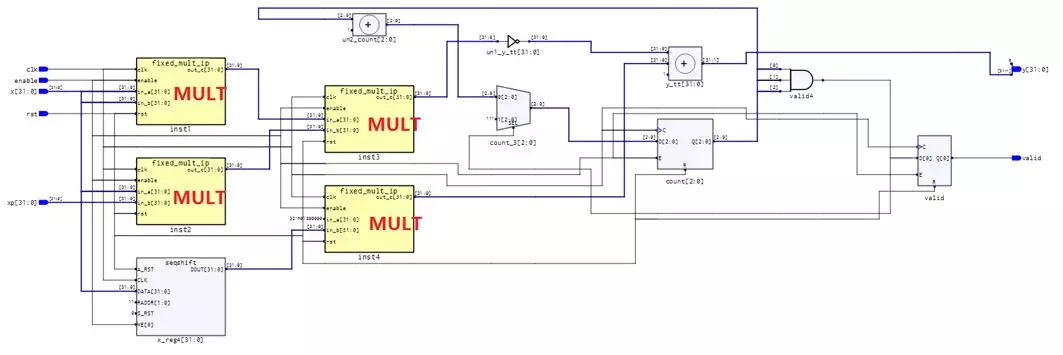
详细信息如下:
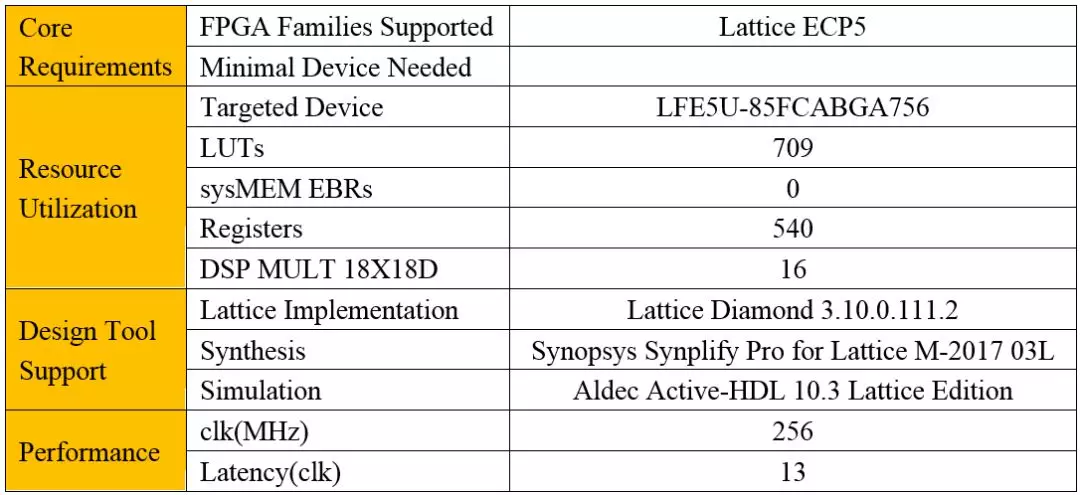
从表中可以发现,Latency从17降低到了13,代价是多使用了一个乘法器模块(4个MULT 18X18D)。其中牛顿迭代的乘法器全部采用了Pipeline结构,并且添加了输入寄存器。如果对频率要求不是特别高的话,还可以将Latency进一步降低到10~11。
3 功能验证与分析
由于程序中仅进行了一次的牛顿迭代,所以结果中存在大约0.2%~0.4%的误差。如果对精度要求较高的话,可以增加一次牛顿迭代。采用Active HDL得到的仿真结果如下:
# KERNEL: Time:299505 ns; Input is 17.500000, Output is 0.238976 # KERNEL: Time:299515 ns; Input is 22.545455, Output is 0.210398 # KERNEL: Time:299525 ns; Input is 6.833333, Output is 0.381974 # KERNEL: Time:299535 ns; Input is 18.076923, Output is 0.235181 # KERNEL: Time:299545 ns; Input is 7.000000, Output is 0.377444 # KERNEL: Time:299555 ns; Input is 6.400000, Output is 0.394654 # KERNEL: Time:299565 ns; Input is 185.000000, Output is 0.073432 # KERNEL: Time:299575 ns; Input is 5.500000, Output is 0.426059 # KERNEL: Time:299585 ns; Input is 20.666667, Output is 0.219894 # KERNEL: Time:299595 ns; Input is 13.500000, Output is 0.272166 # KERNEL: Time:299605 ns; Input is 11.200000, Output is 0.298369 # KERNEL: Time:299615 ns; Input is 16.333333, Output is 0.247126 # KERNEL: Time:299625 ns; Input is 15.142857, Output is 0.256539 # KERNEL: Time:299635 ns; Input is 19.500000, Output is 0.226442 # KERNEL: Time:299645 ns; Input is 11.222222, Output is 0.298077 # KERNEL: Time:299655 ns; Input is 16.500000, Output is 0.245921 # KERNEL: Time:299665 ns; Input is 22.545455, Output is 0.210398 # KERNEL: Time:299675 ns; Input is 10.083333, Output is 0.314373 # KERNEL: Time:299685 ns; Input is 1.000000, Output is 0.998307 # KERNEL: Time:299695 ns; Input is 4.500000, Output is 0.471356 # KERNEL: Time:299705 ns; Input is 6.733333, Output is 0.384780 # KERNEL: Time:299715 ns; Input is 196.000000, Output is 0.071381 # KERNEL: Time:299725 ns; Input is 45.000000, Output is 0.148857 # KERNEL: Time:299735 ns; Input is 38.000000, Output is 0.161977 # KERNEL: Time:299745 ns; Input is 7.000000, Output is 0.377444 # KERNEL: Time:299755 ns; Input is 47.200000, Output is 0.145405 # KERNEL: Time:299765 ns; Input is 12.000000, Output is 0.288423 # KERNEL: Time:299775 ns; Input is 5.142857, Output is 0.440817 # KERNEL: Time:299785 ns; Input is 24.875000, Output is 0.200194 # KERNEL: Time:299795 ns; Input is 8.222222, Output is 0.348593 # KERNEL: Time:299805 ns; Input is 6.200000, Output is 0.400996 # KERNEL: Time:299815 ns; Input is 14.454545, Output is 0.262837 # KERNEL: Time:299825 ns; Input is 11.833333, Output is 0.290408 # KERNEL: Time:299835 ns; Input is 8.307692, Output is 0.346769 # KERNEL: Time:299845 ns; Input is 6.285714, Output is 0.398238 # KERNEL: Time:299855 ns; Input is 10.733333, Output is 0.304720 # KERNEL: Time:299865 ns; Input is 38.000000, Output is 0.161977 # KERNEL: Time:299875 ns; Input is 84.000000, Output is 0.109059 # KERNEL: Time:299885 ns; Input is 29.333333, Output is 0.184446 # KERNEL: Time:299895 ns; Input is 12.500000, Output is 0.282712 # KERNEL: Time:299905 ns; Input is 10.000000, Output is 0.315686 # KERNEL: Time:299915 ns; Input is 9.000000, Output is 0.332953 # KERNEL: Time:299925 ns; Input is 2.000000, Output is 0.706930 # KERNEL: Time:299935 ns; Input is 27.375000, Output is 0.190843 # KERNEL: Time:299945 ns; Input is 27.000000, Output is 0.192154 # KERNEL: Time:299955 ns; Input is 22.400000, Output is 0.211090 # KERNEL: Time:299965 ns; Input is 0.727273, Output is 1.171236 # KERNEL: Time:299975 ns; Input is 1.916667, Output is 0.721861 # KERNEL: Time:299985 ns; Input is 11.000000, Output is 0.301036 # KERNEL: Time:299995 ns; Input is 3.857143, Output is 0.508320 # KERNEL: # KERNEL: ======================================= # KERNEL: Simulation finished Successfully! # KERNEL: ======================================= |

